In this essay, I’ll explain how quantum parallelism can be achieved on a classical machine. Quantum parallelism is usually described as the phenomenon in which a single physical operation, e.g., the execution of a Hadamard gate on an N-qubit memory of a quantum computer, physically affects (updates) the representations of multiple entities, e.g., of all 2N basis states held in quantum superposition in the N-qubit memory. This is the source of the idea that quantum computation is exponentially faster than classical computation. It seems that almost no one working in quantum computing believes quantum parallelism is realizable on classical hardware, i.e., with plain old bits. I believe this is due to the implicit assumption of localist representation in the mathematical formalism, inherited from quantum mechanics, which underlies mainstream quantum computing approaches.
A localist representation is one in which each represented entity is represented by its own distinct representational unit (hereafter “unit” when not ambiguous), i.e., disjoint from the representations of all other entities. The localist representation present in quantum computing is clear in Figure 1. The 2-qubit system of Fig. 1a has 22=4 basis states. Each state is represented by its own symbol, e.g., |00⟩, with its own complex-valued probability amplitude (PA), e.g., α00. Fig. 1b gives the expression for an N-qubit system, which has 2N basis states (assume index var, x, has N places). Figure 1c shows a localist representation of the PAs, and thus, effectively, of the basis states themselves, of the N-qubit system, stored in a classical computer memory. Each PA resides in its own separate physical memory location. Therefore, performing a physical operation on any one PA, e.g., the physical act of changing one of its bits, produces no effect on any of the other 2N-1 PAs. I believe that this localist assumption apparent in Fig. 1c is what underlies the virtually unanimous opinion that simulating quantum computation on a classical machine takes exponential resources, both spatially (number of memory locations) and temporally (number of atomic operations needed).

The “Quantum Leap” in Computing is a Change of Representation, not Hardware
If, instead of localist representations, entities are represented by distributed, and more specifically, sparse distributed, representations (hereafter SDRs), then the power of quantum computation—specifically, quantum parallelism—can be achieved with sub-exponential resources, both in space and time, on a classical machine. As we will see, this is because when entities are represented as SDRs, plain old classical superposition, i.e., representing entities as sets, specifically, sparse sets,of physical objects, i.e., of classical bits, which can intersect, provides the capability described as quantum parallelism.
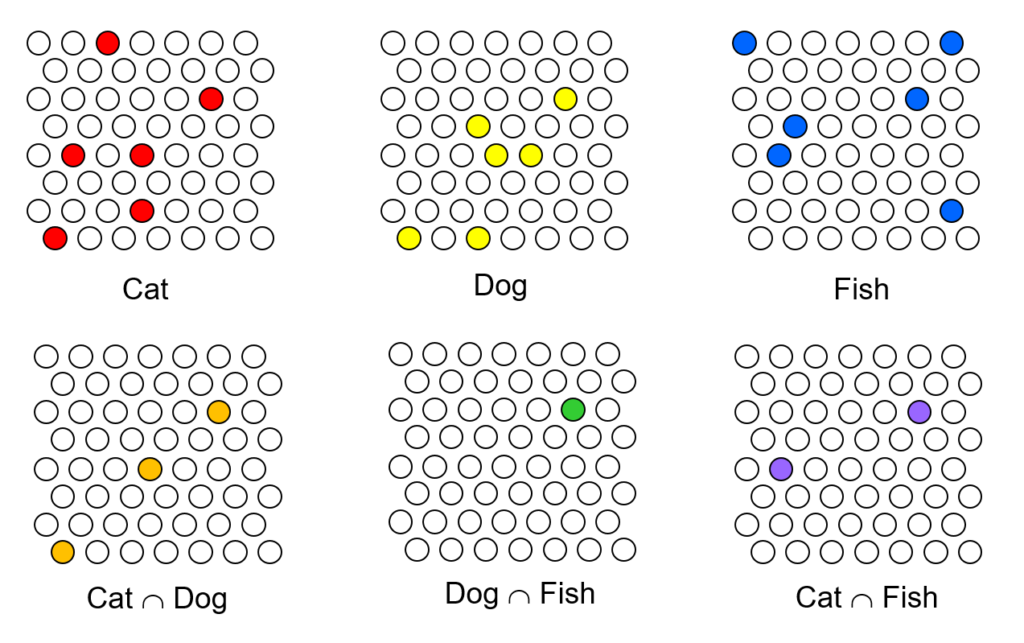
In particular, the SDRs in the model I’ll be describing, Sparsey (1996, 2010, 2014, 2017), are small sets of binary units chosen from a much larger “coding field“, where these SDRs (sets) can intersect to arbitrary degrees. This raises the possibility of using the size of intersection of two SDRs to represent the similarity of the entities (items) they represent. We’ll refer to this property as similar-inputs-to-similar-codes, or “SISC” (n.b.: “code” is synonymous with “representation”). Fig. 2 shows the structure of a Sparsey coding field. Fig. 2a shows one in a linear format: it is a set of Q winner-take-all (WTA) competitive modules (CMs) (red dashed boxes), each consisting of K binary units. Here, Q=7 and K=7 (in general, they can be different). A particular code, consisting of Q active (black) units, one in each CM, is active in the field. N.b.: All codes stored in this field will be of the same size, Q. The total number of unique codes that can be represented, the codespace, is KQ. Fig. 2b shows a 3D view of the field in hexagonal format. It also shows an 8×8 input field of binary pixels, which is fully (completely) connected to the coding field via a binary weight matrix (blue lines). Fig. 2c shows an example active input, A (e.g., a small visual line/edge ), an active code, φ(A), chosen to represent A, and the weights (blue lines) that would be increased (from 0 to 1) from the active input pixels to active coding units, to store A.
Figure 3 (below) illustrates the basis for quantum parallelism in a Sparsey SDR coding field. The top row shows the notional input, A , and corresponding SDR (Code), φ(A), from Fig. 2c. The next four rows then show progressively less similar inputs (measured as pixel overlap), B-E, and corresponding SDRs, φ(B)-φ(E), which were manually chosen to exemplify SISC. The second and last columns show that code similarity, measured as intersection, correlates with input similarity. Note that while the codes were manually chosen in this example, Sparsey’s unsupervised learning algorithm, the Code Selection Algorithm (CSA) (summarized in this section) finds such SISC-respecting codes in fixed-time. The bottom row (below dashed line of Fig. 3) then reveals the following crucial property.
Whenever any ONE particular code is fully active, i.e., all Q of its units are active, ALL other codes stored in the field will also be simultaneously physically active with degree (i.e., strength) proportional to their intersections with the single fully active code.
The likelihood (unnormalized probability) of a basis state is represented by the fraction of its code’s units that are physically active, i.e., by a set of co-active physical units. This contrasts fundamentally to quantum mechanics in which the probability of a basis state is represented by complex number.
For example, the leftmost chart shows that when φ(A) is fully active, φ(B)-φ(E) are active with appropriately decreasing strength. And similarly, when any of the other four codes is fully active (the other four charts). I emphasize that the modular organization of the coding field, i.e., the division of the overall coding field into Q winner-take-all (WTA) modules, is very important. As described here, it confers computational efficiencies over any “flat field” implementation of SDR (as in Kanerva’s SDM model and its various descendants, e.g., Numenta’s HTM). In addition, Sparsey’s WTA module has a clear possible structural analog in the brain’s cortex, i.e., the minicolumn (as discussed in Rinkus 2010). One manifestation of the exponential increase in computational efficiency provided by SDR (assuming the learning algorithm preserves similarity) was previously described in this 2015 post.
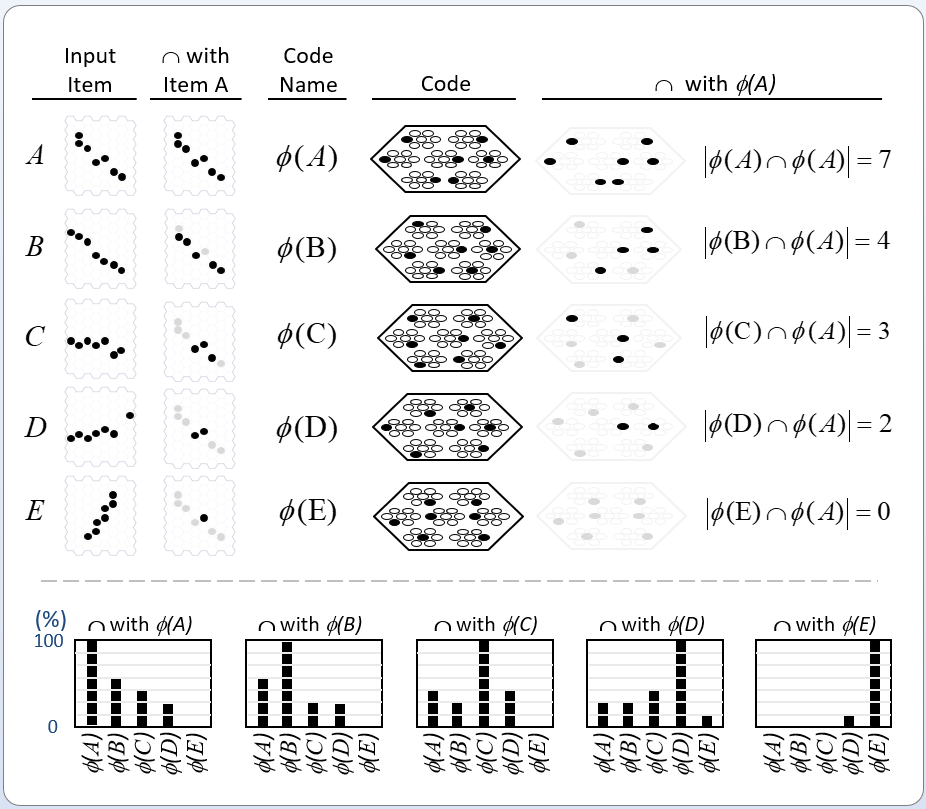
We must take some time to dwell on the property shown in Fig. 3 (and stated in bold above) because it’s really at the heart of this essay and of my argument. It shows that when entities, e.g., basis states, are formally represented as sets, as opposed to vectors (as is the case in quantum mechanics),
purely classical superposition provides the functionality of quantum superposition.
What do I mean by this? Well first, consider Copenhagen, the prevailing interpretation of quantum mechanics (hereafter “QM“). It says that at every moment, ALL basis states of a physical system exist simultaneously in quantum superposition and that there is a probability distribution over those states giving the probability that each particular state would be observed if the system is observed. So that’s the functionality of quantum superposition: allowing ALL physical states to exist in the same space at the same time, with a probability distribution over the states.
The problem is that Copenhagen has never, in a 100 years (!), provided a physical explanation of how multiple different physical states can exist in the same space at the same time. Instead, they have been forced to assert that the probability distribution, which is formally a mathematical, not a physical object, is somehow more physically real than the physical basis states themselves.
Now consider what’s being shown in Fig. 3. It’s purely classical. The individual units are bits, not qubits. Yet, as the charts at bottom of the Fig. 3 show, whenever any one code is active, ALL stored codes are simultaneously proportionally physically active. This constitutes a physically straightforward and immediately apparent explanation of how multiple, in fact, ALL, stored codes, can simultaneously physically exist in the same space, where here, the “space” is the (physically instantiated) SDR coding field. We underscore three keys to this explanation.
- The codes (SDRs) are highly diffuse (sparse).
- The SDRs are formally sets comprised of multiple (specifically, Q) atomic physical units (the binary units of the coding field), or in other words, they are “distributed”. This is essential because it admits a straightforward physical interpretation of what it means for a stored code to be partially active, namely that a code is active with strength proportional to the fraction of its Q units that are active.
- Every code is spread out, again diffusely, throughout the entire coding field. This is enforced by the modular structure of the coding field, i.e., the fact that it is broken into Q WTA modules and every SDR must consist of one winner in each module.
To be sure, in Fig. 3, we’re talking about classical superposition of codes, in particular, of SDRs, which represent physical states (e.g., basis states of an observed system), not about superposition of the physical states themselves. So, we’re not, in the first place, in the realm of QM per se, which was developed as an explanation of physical reality, i.e., of physical objects/systems, and their dynamics, irrespective of whether or not such objects/systems represent information. However, we are exactly in the realm of quantum computing. That is, a quantum computer, like any classical computer, is a physical system for representing and processing informational objects. In a quantum computer, as in any classical computer, it is representations of states (of some other system, e.g., of entries in a database, of states of some simulated physical system, e.g., a system of molecules) and representations of their transitions (dynamics), not the states/transitions themselves, that are physically reified (e.g., in memory).
At the outset, I asserted that the essential problem with mainstream quantum computing is that the founders of QM and of quantum computing were thinking as “localists”. But from another vantage point, the essential problem was the original formalization of QM in terms of vector spaces, specifically Hilbert spaces, rather than sets. In QM, all entities (and compositions of entities, i.e., entities of any scale, from fundamental particles to macroscopic bodies) are formally vectors, and thus are formally equivalent to points, i.e., have the semantics of entities with zero extension. As such it is immediately clear that there can be no formal concept of graded degrees of intersection of entities in QM. It is therefore not surprising that none of the founders of QM, Bohr, Heisenberg, Schrodinger, Born, Dirac—who were all thinking in terms of a vector-based (thus, point-based) formalism—ever developed any physically intuitive (commonsense) explanation of how multiple entities (world states) could simultaneously be partially active (i.e., at different graded levels/strengths) in the same space. This most fundamental of axioms, adopted by QM’s founders, to represent physical entities as vectors, i.e., 0-dimensional points, is precisely what prevented any of those founders from seeing, apparently from ever even entertaining the idea, that classical superposition can provide the full functionality of quantum superposition, and thus can realize can realize what is termed quantum parallelism in the language of QC. But as explained here (most pointedly, with respect to Fig. 3, but throughout), in the realm of information processing, when entities (informational objects) are formally represented as sets, partial (graded) degrees of existence have an obvious and simple classical physical realization (again, as just the fraction of the elements of the set representing an entity that is active). I predict that this change—from vectors to sets, and from localist representations to SDRs—will constitute a “sea change” for quantum computing, and by extension for QM. For yet other implications of the difference between representing entities formally as sets vs vectors, see my earlier post on “Learning Multidimensional Indexes”.
More on the Relation of Quantum Parallelism to the Localist vs. Distributed Representation Dichotomy
Figure 4 revisits Fig. 1 to further clarify why localist representations preclude quantum parallelism. The upper left portion recapitulates Fig. 1 (with a minor change of indexing of units from 1-based to 0-based) and adds an explicit depiction of the memory block for a bottom-up weight matrix (red dashed box) from the input field (for simplicity, the input units are assumed to be binary). We assume the matrix is complete and since the internal representational (i.e., coding) field (black dashed box) is localist, that matrix has M x 2N weights. The lower middle portion shows the coding field, now denoted A, again, and where, for concreteness, we assume there are N=3 input units. Thus, there are 23=8 possible input (basis) states and each has its own memory location. We show a particular probability distribution over those states at time t: the values sum to 1, and |100⟩ is most likely. We then introduce another matrix (green), a recurrent matrix that completely connects A to itself. The idea is that signals originating at time t recur back to A at t+1 whereupon some processing occurs in the coding field (in particular, including all 23 units computing their input summations), resulting in an updated probability distribution over the states at t+1. This recurrent matrix is 2N x 2N, and corresponds to a unitary operator of QM, and this will be discussed further in relation to Fig. 5. The red boxes identify the two essential weaknesses of localist representations with respect to quantum parallelism. First, as pointed out in the lower red box, and as stated at the outset, applying a physical operation on any one memory location, changes the value of only the one basis state represented by that location. Consequently, updating all 2N basis states requires 2N physical operations. Second, as pointed out in the upper red box, applying a physical operation to change the signal value on any one (bolded green line) of the 2N x 2N recurrent connections (or to change the weight of the connection) affects only the one basis state at the terminus of that connection. Clearly, it is the localist representation per se, that precludes the possibility of quantum parallelism.
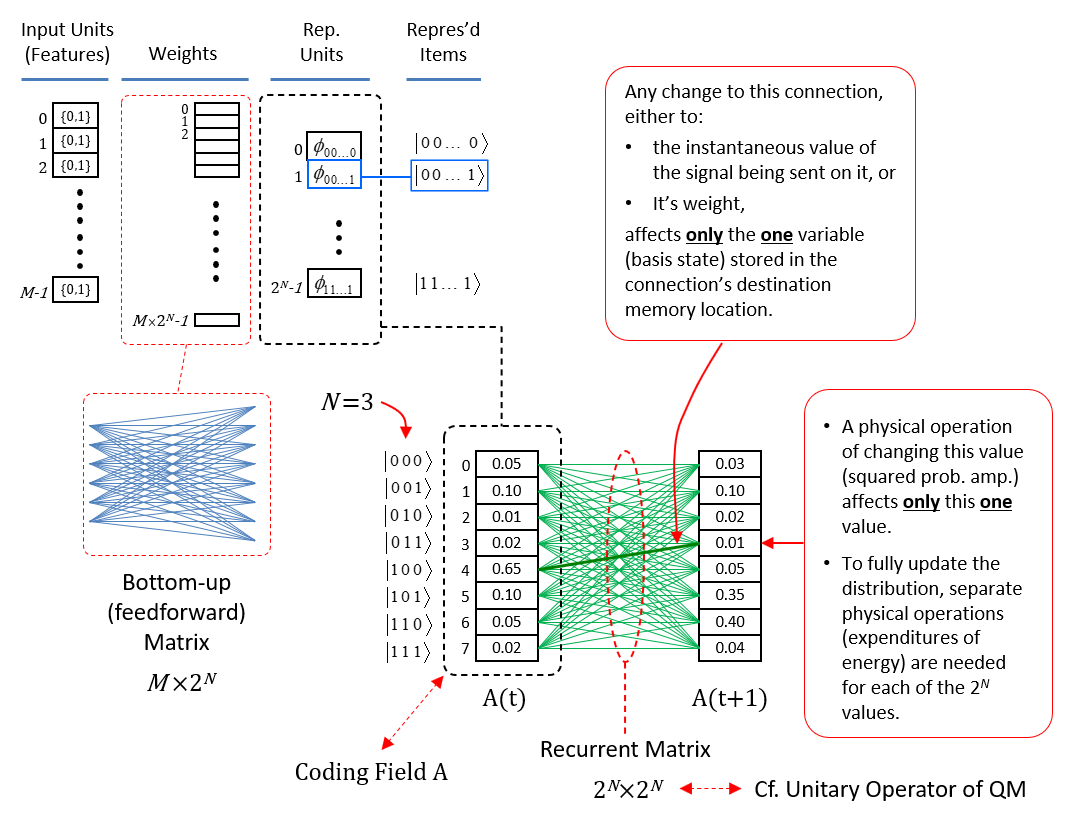
Figure 5 now shows the physical realization of quantum parallelism when items are represented as SDRs. As the “Representational Units” column shows, in the SDR case, the coding field is now organized as Q blocks of memory [the competitive modules (CMs) described above], each with K memory locations (which, in this case, can literally be just single bits), for a total of QK locations. Again, assuming N=3 input units, the next column shows the 23 represented items, i.e., basis states, and the colored lines between the columns show (notionally) the SDRs of three of the represented states. The blue arrows show that the code of |000⟩, φ(|000⟩), consists of the second unit in CM q=0, the second unit in CM q=1, …, and the last unit in CM, q=Q-1. The red arrows show the code for |110⟩, φ(|110⟩), which intersects with φ(|000⟩) in CM q=1, and so forth. The bottom right portion of the Fig. 5 shows the coding field again, where for concreteness, Q=5 and K=3, and shows the completely connected recurrent matrix (green). Note in particular, that the number of weights, (QK)2, in the recurrent matrix no longer depends on the number of represented (stored) basis states as for the localist case in Fig. 4. To the right, we see three possible states of the coding field, i.e., concrete codes for the three (out of 23) basis states above.
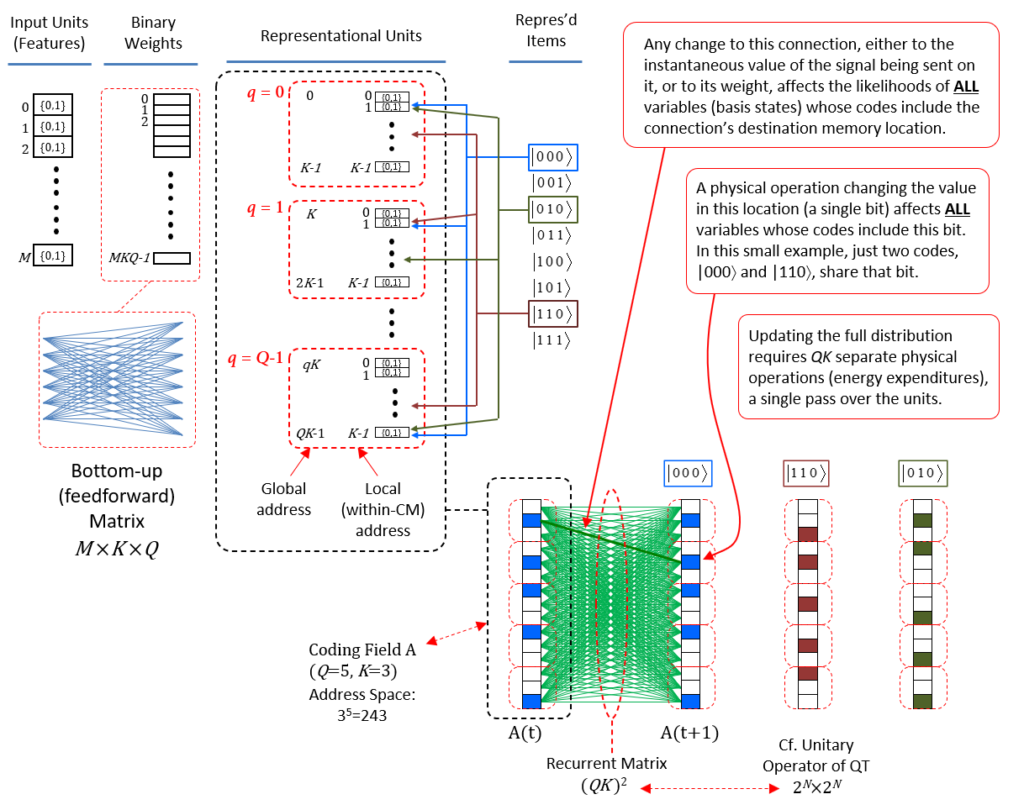
The red boxes of Fig. 5 explain how quantum parallelism is realized in the case of SDR. The middle red box explains that when a physical operation is applied to any one unit of the coding field, in particular, the second unit of CM 1 (red arrow), ALL represented basis states whose SDRs include that unit are necessarily changed. For example, if the operation turns this unit off, then not only is the state, |000⟩, less strongly present, but so is the state, |110⟩: a single expenditure of energy at a particular point in space, a single bit, physically updates the states of multiple represented entities, i.e., quantum parallelism. This example clearly shows that using SDR implies quantum parallelism. The lower red box then explains that making a single pass over the QK memory locations, thus, QK physical operations, necessarily updates the full distribution over all stored codes. The crucial question is then: how many SDRs can be stored in such a field, or more specifically, how does the number of codes (i.e., of represented basis states of some observed/modeled system) that can be safely stored grow as a function of QK? As described below (Fig. 9), the results from my 1996 PhD thesis show that that number grows super-linearly in QK.
Finally, the upper red box of Fig. 5 explains that applying a single physical operation to any one connection (weight) necessarily affects ALL SDRs that include the unit at the terminus of that connection: again, this is quantum parallelism, but operating at the finer scale of the weights as opposed to the units. For example, if the weight of the bold green connection is increased (assume real-valued wts for the moment), then the input summation to its terminus unit (second unit in CM 1) will be higher. Since the CM functions as a WTA module, where the winner is chosen as a draw from a distribution (a transformed version of the input summation distribution), that unit will then have a greater chance of winning in CM 1. Thus, every SDR that includes that unit will have a greater likelihood of being activated as a whole, all from a single physical operation applied to a single memory location (representing a single weight). [The algorithm is summarized below.]
The Recurrent Matrix Embeds State Transitions that are Analogs of Unitary Operators of QM
I said above that the recurrent matrix corresponds to a unitary operator of QM. More precisely, the recurrent matrix is a substrate in which (in general, many) operators are stored, i.e., learned, during the unsupervised learning process. However, note that in QM, an operator is the embodiment of physical law (i.e., time-dependent Schrodinger equation) and is NOT viewed as being learned. Moreover, the approach of mainstream quantum computing has largely been to DESIGN operators, i.e., quantum gates and circuits composed of such gates, which perform generic logical operations; again, no learning.
Therefore, in yet another major departure from quantum mechanics and from mainstream quantum computing, in the machine learning (specifically, Sparsey’s unsupervised learning) scenario described here, the operators ARE learned from the data.
To flesh this out, let’s consider the case where the inputs are spatiotemporal patterns, e.g., sequences of visual frames as in Fig. 6. The figure shows a Sparsey coding field (rose hexagon), comprised of Q=7 WTA CMs, each composed of K=7 binary units, experiencing three successive frames of video of a translating edge in its input field, i.e., its “receptive field” (green hexagon). The coding field chooses an SDR (black units) for each input on-the-fly as it occurs and increases, from 0 to 1, all recurrent weights from units active at T to units active at T+1 (green arrows, and only a tiny representative sample shown, and in general, some may already have been increased by prior experiences).. Thus, input sequences are mapped to chains of SDRs (further elaborated on here, here, here, and most thoroughly, in my 2014 paper).
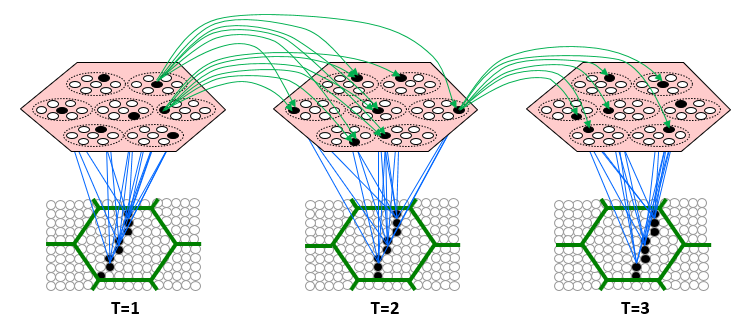
Fig. 6 depicts Sparsey’s primary concept of operations, i.e., to automatically form such SDR chains (memory traces) in response to the input sequences it experiences. But consider just a single association formed between one input frame and the next, e.g., between T=1 and T=2 of Fig. 6. This association, which is just a set of increased binary weights, can be viewed as an operator. It’s an operator that is formed, with full strength based on the single occurrence of two particular, successive states of the underlying physical world. From the vantage point of traditional statistics, this is just one sample and in general, we would not want to embed a memory trace of this at full strength: after all, it could be noise, e.g., it could reflect accidental alignments of one of more underlying objects and thus not reflect actual (or in any case, important) causal processes in the world. Nevertheless, Sparsey is designed to do just that, i.e., to embed this state transition as a full strength memory trace based on its single occurrence. It’s true that such an operator (state transition) is therefore highly idiosyncratic to the system’s specific experiences. However, because:
- all such state-to-state transitions, which again are physically reified as sets of changed synaptic weights, are superposed (just as the SDRs themselves are superposed), and
- Sparsey’s algorithm for choosing SDRs, the Code Selection Algorithm (CSA), preserves similarity (see below)
subsets of synapses that are common to multiple individual state-to-state transitions come to represent more generic causal and spatiotemporal similarity relations present in the underlying (observed) world. Hence, Sparsey’s dynamics realizes the continual superposing of operators of varying specificities directly on top of each other. Many/most of the more specific ones (akin to episodic memories) will fade with time, leaving the more generic ones (akin to semantic memories) in their wake.
Finally, what about the unitarity requirement of QM’s operators? That is, QM allows only unitary operators, i.e., operators that preserve a norm. This is required because the fundamental entity of QM is the probability distribution that exists over the basis states of the relevant physical system. Thus, in QM, all physical actions MUST result in a next state of the physical world that is also characterized by a probability distribution, i.e., must preserve the L2 norm to be of length 1. However, as noted above, e.g., with respect to Fig. 3, the instantaneous state of a Sparsey coding field, which is always a set of Q active binary units, represents a likelihood distribution over the stored codes. The likelihoods are fractions between 0 and 1, but do not sum to 1. Indeed, the total sum of likelihoods will in general change from one time step to the next. Of course, the vector of likelihoods over the stored codes can in principle, always be normalized (by dividing them all by the sum of all the likelihoods) to produce a true probability distribution. However, Sparsey’s update dynamics (see next section) effectively achieves this renormalization without requiring that explicit computation.
Summary of Sparsey’s Code Selection Algorithm (CSA)
The key innovation of Sparsey is a simple, general, single-trial (one-shot), and most importantly, “fixed-time” unsupervised learning (storage) algorithm, the Code Selection Algorithm (CSA), which preserves similarity from the input space to the code (SDR) space, i.e., maps more similar inputs to more similar, i.e., more highly intersecting, SDRs. Fig. 7 illustrates this algorithm. The example involves a tiny instance of a Sparsey coding field comprised of Q=5 WTA CMs, each with K=3 units, and which receives a complete binary matrix (all wts initially 0, light gray) from an input field having 8 binary units. The top panel (at left) shows the four inputs, A to D, that will be considered. Note that we constrain all inputs to be of the same size, i.e., 5 active units, and that inputs B to D are progressively less similar to A. In the top panel (center), we show the act of learning input A: A is presented, an SDR, φ(A), is chosen by randomly picking a winner in each CM, and all weights from active input units to active coding units are increased from 0 to 1 (a simple Hebbian learning rule). A is the only input that will be learned in this example: the remaining four panels (1-4) illustrate the cases of presenting A, B, C, or D, as a test input, after having learned only A.
While the text in the Fig. 7 fully explains the dynamics, I’ll walk through it in the text here too. In Panel 1, we present A again. Due to the learning that occurred in the learning trial, the bottom-up (u) input sum will be u=5 for the five units that were randomly chosen to be in φ(A) and u=0 for all other units (shown in the yellow bar charts above the CMs). Clearly, if this model is being used as an associative memory, we would want the code originally assigned to this input, φ(A), to be activated exactly again. That would constitute the model recognizing the input. In this particular case, the model could achieve this by simply activating the unit with the hard max input sum (u) in each CM. However, for reasons that will be made clear in the remaining panels, Sparsey works differently. Rather, what Sparsey does is transform the u vector in each CM into a probability (ρ) distribution and then draw the winner from that distribution (i.e., a soft max in each CM). Here for example, the transform applied in each CM gives a little probability to each of the u=0 units, but most to the u=5 unit. In other words, the u distribution is slightly compressed (flattened, whitened) to yield the ρ distribution. In this case, we expect the max-ρ unit to win in most of the CMs, but lose occasionally (an exact expectation could be computed as a Bernoulli distribution, but that detail is not important to illustrate the essential concept of the algorithm). For argument’s sake, in this case, we show the max-ρ unit actually being chosen in all Q CMs, i.e., perfect reactivation of φ(A).
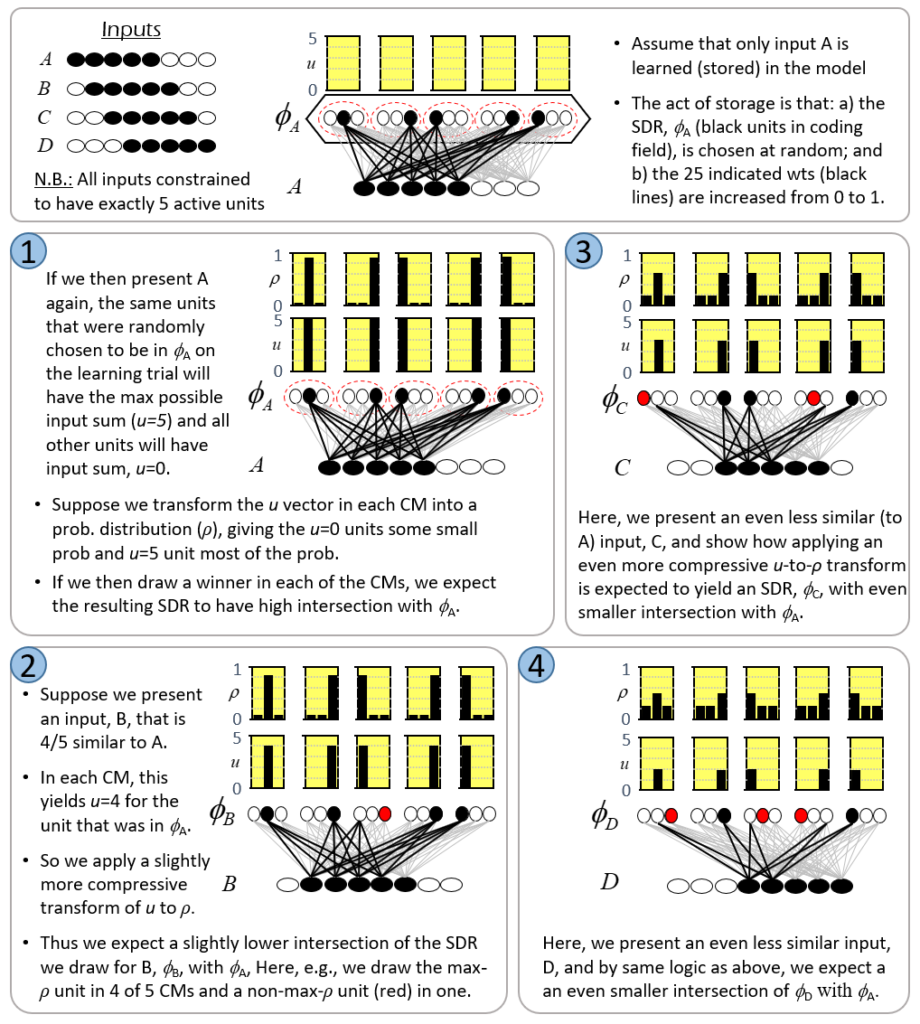
In Panel 2, we present a novel input, B, which is very, i.e., 4/5, similar to A. In fact, the model cannot know whether B is a truly novel input, i.e., whether its featural difference from A has important consequences and thus, whether B should be stored as a unique input, or whether B is a just a noisy version of A, in which case, A’s code, φ(A), should just be reactivated exactly. This is a meta-question (addressed for example in my 1996 thesis), but for the sake of this example, let’s assume it’s a truly novel input. In this case, despite the fact that we want to assign a unique code, φ(B), to B, we nevertheless should want φ(B) to be similar to φ(A), which in the case of SDRs, means having a high intersection. Following the reasoning given for Panel 1, we can achieve this result, i.e., approximately preserve similarity, by simply applying a slightly more compressive transform of u to ρ distributions in each CM (i.e., assign slightly more probability of winning to the u=0 units than in Panel 1, but still, much more probability of winning to the u=5 unit), as shown in Panel 2. For argument’s sake, we show the max-ρ unit winning in 4 out of 5 CMs, and the non-max-ρ unit (red unit) winning in one CM. Thus, B is 80% similar to A, and φ(B) is 80% similar to φ(A). The fact that the input and code similarities are both 80% here is incidental. What’s important is just this general principle that if we simply make the degree of compression of the u-to-ρ transform be inversely related to input similarity (directly proportional to novelty), we will approximately preserve similarity. Panels 3 and 4 just illustrate the same reasoning applied to progressively less similar inputs as the figure’s text explains. Hopefully, it is now clear why winners must be chosen using soft max rather than hard max: if hard max was used to pick the winner in each CM in panels 2-4 of Fig. 7, then the same exact SDR would be assigned to all four inputs. If the goal is to ensure (approximately) SISC, then soft max must be used.
Fig. 7 illustrates the essential concept of Sparsey’s Code Selection Algorithm (CSA), which can be described simply as: adding noise into the process of selecting winners (in the CMs), the magnitude (power) of which varies directly with the novelty of the input. Or, we can describe this as increasing noise relative to signal, where the signal is the input (u) vector (which reflects prior learning), again, proportional to input’s novelty. As the power of the noise increases relative to that of the signal, the ρ distributions approach the uniform distribution, thus, the selected SDR becomes completely random. This implements the clearly desirable property that more novel inputs are mapped to SDRs with higher expected Hamming distance from all previously stored SDRs, which maximizes expected retrieval accuracy. In contrast, the more similar a new input, X, is to one of the stored inputs, Y, the less noise is added to the ρ distributions and the greater the probability of reactivating the SDR of Y, φ(A), and in any case, the higher the expected fraction of φ(A) that will be reactivated.
Fig. 7 showed how increasingly novel inputs are mapped to increasingly distant (in terms of Hamming distance) SDRs. But how is novelty computed? It turns out that there is an extremely simple way to compute novelty, or rather to compute its inverse, familiarity, which was also introduced in my 1996 thesis (and described in subsequent works, 2010, 2014, 2017). I denote the familiarity of an input as G, which is simply the average of the max u values over the Q CMs. In fact, G reflects not merely the similarity of a new input, X, to the single closest-matching stored input, but it computes a generalized familiarity of X to ALL the stored inputs. That is, it reflects the higher-order similarity structure over all stored inputs. A G-like measure of novelty/familiarity appeared in a recent Nature article (Dasgupta et al, 2017) as part of a model of fly olfactory processing [the authors were unaware of my related method from 20+ years earlier (personal communication)]. However, the Dasgupta model does not use G to ensure (approximate) similarity preservation as does Sparsey.
Fixed-time Update of Likelihood Distribution over All Stored Codes
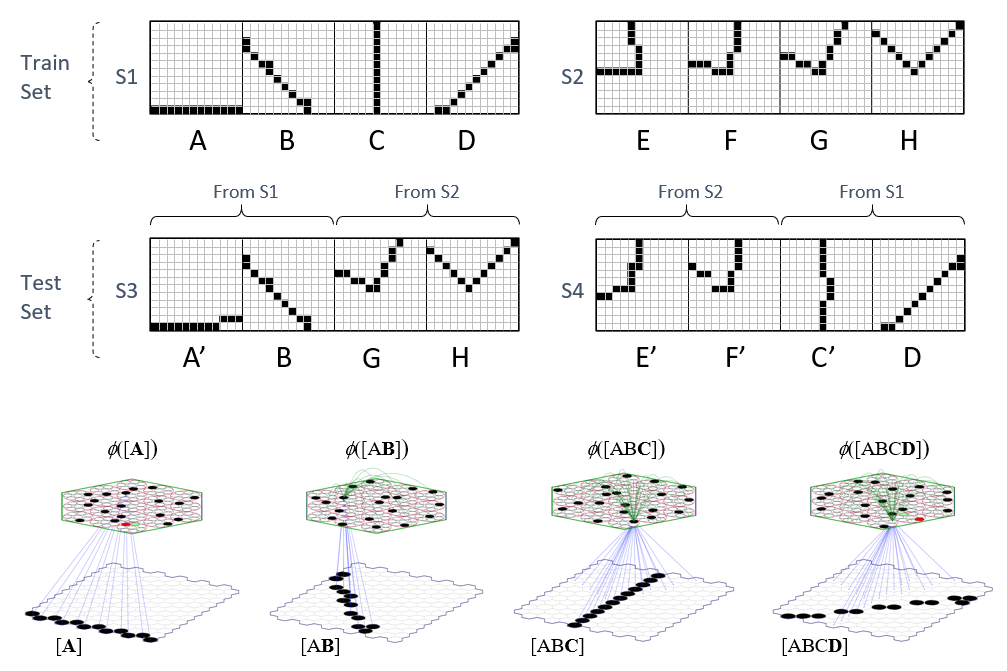
This section is currently just a stub. It will present results from my 2017 paper “A Radically New Theory of how the Brain Represents and Computes with Probabilities”, demonstrating fixed-time update of the likelihood distribution (and indirectly, the total probability distribution) over ALL items stored in a coding field. Moreover, these results concern learning and inference over spatiotemporal patterns, i.e., sequences, not simply spatial patterns as in the prior section. This entails a generalization of the CSA (compared to that described with respect to Fig. 7) in which the SDR chosen for the input at time t depends on both the bottom-up signals (the u values) and the signals arriving via the recurrent (a.k.a. “horizontal”) matrix (green arrows) from the code at time t-1. Note however, that the generalized CSA remains a fixed-time algorithm. The training set used in that paper consists of the two sequences, S1 and S2, shown in Fig. 8. The test sequence, S3, consisted of the first two items of S1 followed by the last two items of S2, the idea being that we “garden path” the model and see how well it can recover when it encounters the anomaly. Test sequence S4 was comprised of the first two items of S2 and the last two of S1. And, we also added some pixel-wise noise to some of the test sequence frames to make the inference problem harder. At bottom of Fig. 8, we show the model on the four items of training sequence S1, showing the bottom-up weights that were increased on each frame and a subset of the recurrent weights (green) that were increased. The full description of this result would make this already very long blog much longer and so will be done in a separate blog. For now. the reader can look at the 2017 paper to see the full description. As you will see, Sparsey, easily deals with these ambiguous moments of sequences, and rapidly recovers into the correct internal SDR chain as subsequent items of the sequence come in.
Further Remarks on Algorithmic Parallelism vs. Quantum Parallelism
As noted at the outset, with respect to an N-qubit quantum computer, quantum parallelism is usually described as the phenomenon in which the execution of a single physical, atomic operation simultaneously operates on all 2N basis states in the superposition. For example, applying a Hadamard transform on the N qubits results in a physical superposition in which all 2N basis states have equal probability amplitude, thus equal probability. More generally, in an instance of the Deutsch-Jozsa algorithm, a circuit of quantum gates is designed that computes some function, f(). A single physical application (execution) of that circuit on the N-qubit system operates on all 2N basis states, φi, held in superposition, yielding a new superposition of the 2N values, f(φi). I make two key observations about this description of quantum parallelism.
- I emphasized “designed” above to highlight the fact that most of the work in quantum computing has not focused on learning. Ideally, we want learning systems, and in particular, unsupervised learning systems, that realize/achieve quantum parallelism. That is, what we ideally want is a computer that can observe a physical dynamical system of interest through time—e.g., multivariate time series of financial/economic data, or biosequence/medical data, video (frame sequences) of activities/events transpiring in spaces, e.g., airports, etc.—and learn the dynamics from scratch. By “learn the dynamics”, I mean learn the “basis states” of the system and learn the likelihoods of transitions between states, all at the same time.
- In the above description of quantum parallelism, a single atomic physical operation is described as operating on, i.e., updating the probability amplitudes of, all 2N basis states held in the superposition in the N qubits. However, if these basis states in fact represent the states of a natural physical system, then while it is true that there are formally 2N basis states, almost all of them will correspond to physical states that have near-zero probability of ever occurring. Moreover, almost all of the 2N x 2N state transitions will also have near-zero probability of occurring. That is, the strong hierarchical part-whole structure of natural entities and natural dynamics, e.g., operation of natural physical law, will, with probability close to 1, never bring the system into such states. These states likely do not need to be explicitly represented in order for the model to do a good job emulating the system’s evolution through time, and thus, allowing good predictions. Thus, if we take “almost all” seriously, then the number of basis states that, in practice, need to be represented (held) in superposition may be exponentially smaller than 2N, i.e., polynomial (and perhaps low-order polynomial) in N.
Sparsey addresses both these observations. Regarding the first, Sparsey was developed from inception as a biologically plausible, neuromorphic model of learning [as well as of memory (both episodic and semantic), inference, and cognition] of spatiotemporal patterns (handling purely spatial patterns as a special case). In that domain, the represented entities are sensory inputs, e.g., visual input patterns (preprocessed as seen here, here, or here), which are not known a priori, but have to be learned by experiencing the input domain, i.e., the “world”. In contrast, in quantum mechanics, the entities are the physical basis states themselves, which are defined a priori, in terms of the values of (generally, one or a few) fundamental physical properties, e.g., spin angular momentum, polarization, of the system’s atomic constituents. Thus, quantum mechanics proper, has NOT been a theory about learning. Not surprisingly, quantum computing has largely also NOT been about learning. Most quantum computing algorithms in the literature, e.g., Shor’s, Grover’s, are fixed algorithms that perform specific computations.
Regarding the second observation, a Sparsey coding field has a large storage capacity, not exponential in the units, but large. Specifically, simulation results show faster than linear (i.e., as some low-order polynomial) capacity scaling in the units, and linear scaling in the weights. N.b.: Those results from my 1996 Thesis research were done on a slightly different architecture. While they apply with full force to the current architecture (see Fig. 2), I don’t want to introduce the older architecture in the main flow of this essay and so direct the reader to this page to see the detailed results. Fig. 9 summarizes those results. In these experiments, the coding field consisted of Q=100 WTA CMs, and the number of units per CM, K, was varied from 8 to 40 in steps of 4. Here, the relevant matrix was the recurrent matrix that fully connected the coding field units to themselves. Thus, the matrix for the largest model tested, whose coding field had 100×40=4000 units, had 16 million weights. The learning protocol was temporal Hebbian, i.e., all weights from units active at T to units active at T+1 were set to 1 (either increased from 0 to 1, or left at 1). Thus, the SDRs of successive items of a sequence were “chained” together (as in Fig. 6). Also, in these experiments, the input level was a 10×10 binary pixel array and the objective was to store as many as possible 10-frame-long sequences, where each frame had 20 active pixels, as shown in Fig. 9a.
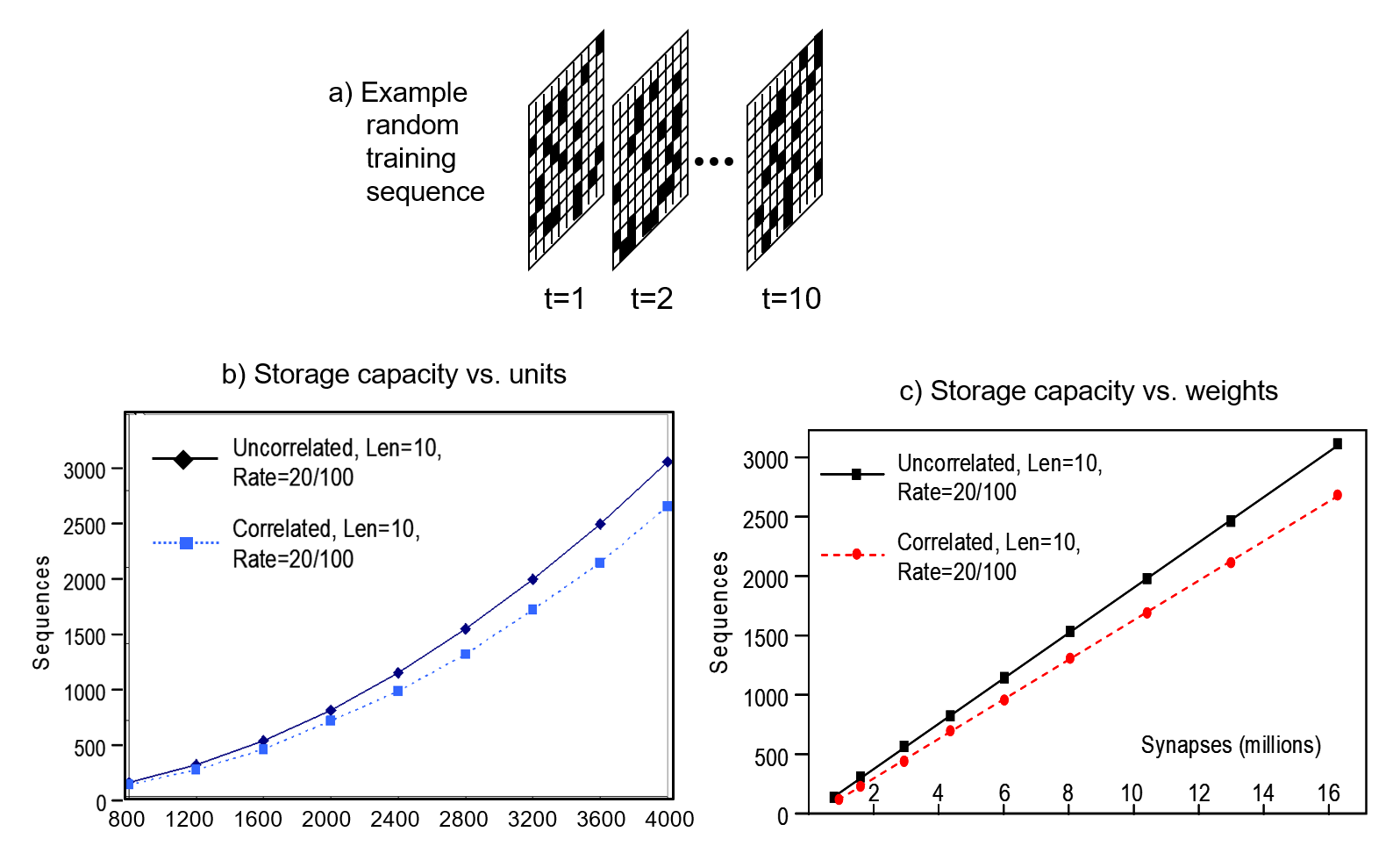
Two input conditions were tested. In the first, labelled “uncorrelated”, all frames of all sequences were generated randomly. In the second, labelled “correlated”, we first created a lexicon of 100 frames, that were also generated randomly. The actual sequences of the correlated training set were then created by making 10 random draws (with replacement) from the lexicon. This “correlated” condition was intended to model the linguistic environment, i.e., where the items of sequences occur numerous times and in numerous sequential contexts. As Fig. 9b shows, the number of such sequences that can be safely stored, i.e., stored so that all sequences can be retrieved with accuracy above some threshold, here, ~97%, grows faster than linearly in the units. Note that here, retrieval was tested by reinstating the code of the first item of a sequence and measuring how precisely the remaining nine items were read out, i.e., these were recall, not recognition, tests. So this is a lot of information being stored and recalled. In the largest model tested (4000 units, 16 million wts), over 3,000 of these random 10-frame sequences were safely stored, despite being presented once each. Fig. 9c shows that the capacity scales linearly in the weights.
The classical realization of quantum entanglement
Quantum entanglement (QE) is the phenomenon in which two particles, X and Y, become perfectly correlated (or anti-correlated) with respect to some property, e.g., spin, even though neither particle’s value of that property is determined. In fact, the only definite physical change that can be said to occur at the moment of entanglement is that a dependence is introduced between X and Y such that if one is subsequently measured and found to have spin up, the other will instantly have spin down. X and Y are said to be in the “singlet” state: they are formally considered to be a single entity. At the moment of measurement, X and Y become unentangled, i.e., the singlet state, which is a superposition of the two basis states, collapses (decoheres) to one of the two possible basis states. This phenomenon occurs regardless of how far apart X and Y may be when either is measured, which implies superluminal propagation of effect (transfer of information), i.e., Einstein’s “spooky action at a distance”.
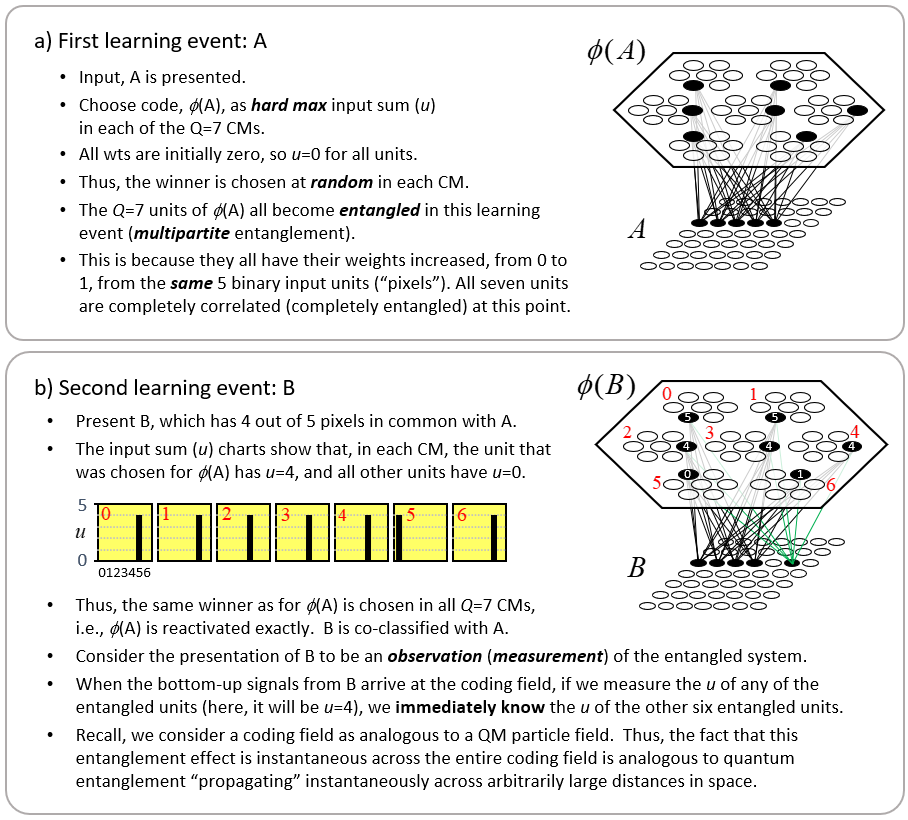
Is there another way of understanding the phenomenon of QE? Yes, I will provide a new, classical explanation of QE here, in terms of Sparsey’s SDR codes and the weight matrices that connect (including recurrently) coding fields. First, recall, in a side comment above, I proposed that a Sparsey coding field is the analog of a QM particle field, let’s say, the electron field. Thus, Sparsey’s binary units should be viewed as analogs of QM’s electrons. Fig. 10 illustrates the phenomenon of entanglement in Sparsey. Note however that this example uses a simpler code selection algorithm than Sparsey’s actual CSA, described above. Specifically, winners will now be chosen using hard max instead of soft max. Fig. 10a shows the learning event in which an input pattern, A (the five active binary units, “pixels”), has been presented. Note that all inputs will be constrained to have the same number of active pixels. The code (SDR), φ(A), is then chosen by picking the unit with the hard max input sum (u) in each CM. Since all weights are initially zero, all units have u=0, so the winners (black) are chosen randomly. Finally, the association from A to φ(A) is formed by increasing the depicted weights (black lines) from 0 to 1. The Q=7 units comprising φ(A) become entangled in this learning event. They become entangled because their individual afferent weight matrices are changed in exactly the same way: they all have their afferent weights from the same five active pixels increased from 0 to 1. Note also that at this point, these seven units are completely redundant (completely correlated).
To see why this learning event constitutes entanglement, consider the presentation of a second input, B, in Fig. 10b. B has 4 out of 5 pixels in common with A. Suppose we can observe (measure) any of φ(A)’s units, i.e., we have an “electrode” in it. Then, when the bottom-up signals arrive from the input level, as soon as we measure u for any one of those units, and find it to have u=4, we instantly know the other six units of φ(A) also have u=4. Just as in QM, where entanglement “propagates” across arbitrarily large distances of an actual quantum field, which spans all of space, this example shows that entanglement “propagates” across the full extent of of the coding field. But unlike the case for QM, we can directly see the physical mechanism underlying this “propagation”. In fact, it is clear that it is not propagation at all: no signal propagates across the coding field in this scenario. Again, it’s simply the correlated changes that occurred in the weight matrix that impinges the coding field during the learning, i.e., entanglement, event, which explains how we can instantly know the value of some variable (u) at arbitrarily remote distances from where a measurement takes place.
So, what is this telling us? It’s telling us that the weight matrix is analogous to a force-carrying (boson) field of QM. After all, it’s the boson fields through which effects (information) propagates through space and its the weight matrices of Sparsey (or of any neuromorphic model) through which effects/information propagate. I further emphasize that a boson field fills all of space (and is superposed with all other boson and fermion fields) and in particular, allows transmission of an effect from any point in space to any other (at ≤ speed of light). In other words, a boson field completely connects any particular fermion field. Likewise, we require that the matrix between any two Sparsey coding fields (including recurrently) and between a coding field and an input field also be complete. But of course there is at least one huge difference between a boson field and a weight matrix. The individual weights comprising a Sparsey weight matrix are changed by the signals that pass through them. In contrast, no such concept of learning, at least of permanent learning, applies to a boson field. I believe this is at the heart of why no one has have ever figured out a local “hidden variables” (HV) mechanism for QM. In all discussions I’ve seen, it seems that any such local HVs were posited to be located within the particles themselves. Recent experiments showing violation of Bell’s inequality refute those types of local HV explanations. But again, in Sparsey, as shown in Fig. 10, the physical changes underlying entanglement occur outside the entangled entities (the units) themselves; they occur in the weights. These weights still constitute local variables [after all, any individual weight is immediately local (adjacent) only to its source and destination units], but they are not hidden variables. I suspect that the recent Bell inequality violation findings do not refute the type of “local variables” explanation given here.
There is a great deal more to present regarding this new explanation of QE. I’ll do that in subsequent posts. For now, I just want to end this section by noting that this same principle/mechanism applies when thinking about how groups of neurons somehow become bound together to act as an integral code (single entity), i.e. how Hebbian “cell assemblies” form. Most prior computational neuroscience theories for cell assemblies, e.g., Buszaki’s “Synapsembles” (2010), propose that they form by virtue of changes made to weights directly between the member units of the cell assembly. But I have previously described how the “binding” mechanism described here–correlated changes to afferent and efferent weight matrices of the bound units–could easily explain the formation of cell assemblies in the brain’s cortex.
Summary
Coming soon…..