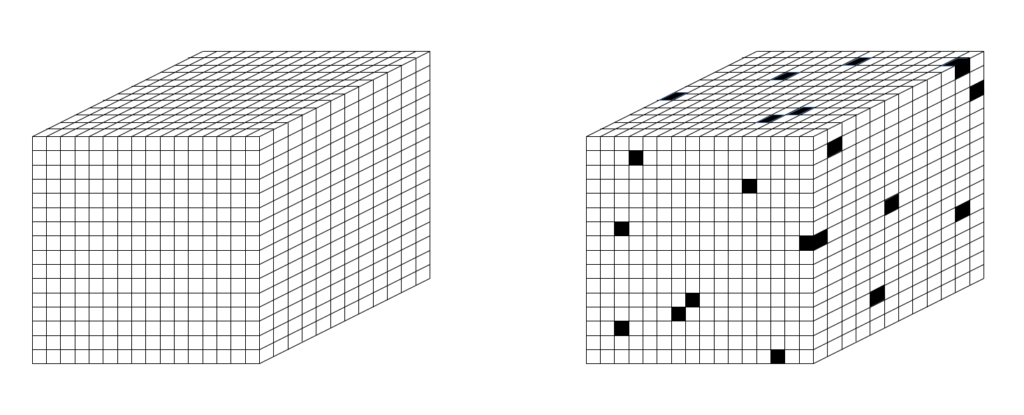
The holographic principle says that the maximum amount of information that can be contained in a volume (bulk) equals the amount of information that can be contained on the surface of that bulk. On first thought, this seems absurd: Common sense tells us that there is so much more matter comprising a bulk than comprising its surface. Yet, this is what the work of ‘t Hooft and others tells us. Fig. 1 (from ‘t Hooft’s 2000 paper, “The Holographic Principle”) shows a tiling in which each patch, of area equal to 4 x Planck area (~4 x 10-70 sq. m.), can hold one bit of information. Since black holes are the most dense objects, we can take this number, the area of the surface of a spherical volume in units of Planck areas divided by 4 to be an upper bound on the number of bits that can be stored in that volume. In fact, the explanation given in this essay suggests the upper bound is just slightly less than the area in Planck units.

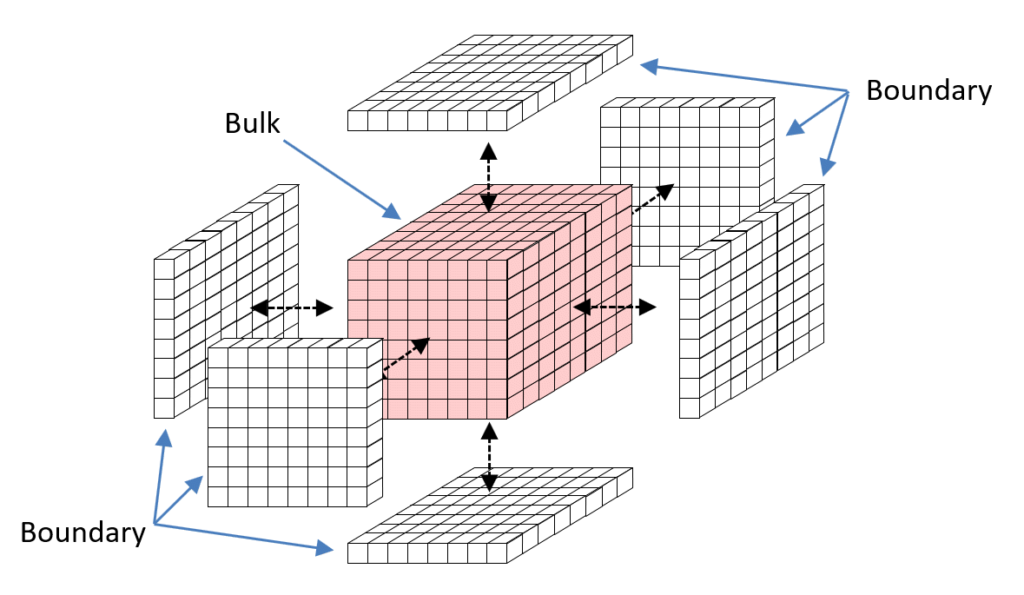
If the Planck length is the smallest unit of spatial size, then 2D surfaces in space have areas that are discretely valued and 3D regions have volumes that are discretely valued. Since the cube is the the only regular and space-filling polyhedron for 3D space, we therefore assume that space is a cubic tiling of Planck volumes as in Fig. 2. If the Planck volume is the smallest possible volume then it can have no internal structure. Thus, the simplest possible assumption is that it is binary-valued; either something exists in that volume (“1”) or not (“0”). I call these Planck-size volumes, “Planckons”. However, note that despite the ending “ons”, these are not particles like those of the Standard Model (SM). In particular, they do not move: they are the units of space itself.
I contend that that the this assumption, that space is a 3D tiling of binary-valued Planck cubes already explains the why the amount of information that can be contained in a volume is upper-bounded by the amount of information that can be contained on its surface, i.e., the holographic principle. For example, consider a cube-shaped volume of space, i.e., a bulk, that is 8 Planck lengths on each side, as shown in Fig. 3 (rose colored Planckons). This bulk, consists of 83 = 512 Planckons. Consider the layer of Planckons that forms the immediate boundary of this bulk. We can take the boundary to be just the union of the six 2D arrays of Planckons that are immediately adjacent to the six faces. Thus the boundary consists of 6 x 82 = 384 Planckons. In the case of a black hole, this boundary is the event horizon. The reason why we ignore the Planckons that run along just outside the edges of the bulk and those at the corners just outside the bulk is that we assume that physical effects can only transmit through faces of Planckons.. The boundary constitutes a channel through which all physical effects, i.e., communication (information), to and from this bulk must pass. The number of unique states that the bulk can be in is 2512. On first glance, this suggests, that the amount of information that can be stored in this bulk is log22512bits, i.e., 512 bits. The number of unique states of the channel is only 2384, suggesting it can hold only log22384 = 384, bits of information. In fact, the holographic principle says that the number of bits storable in the channel is only 384 / 4 = 96 bits. However, the explanation developed here suggests the limit is just less than 384. The reason it’s not exactly equal to to 384 is a slight diminution due to edge and corner effects. In any case, the overall argument explains why the information storage capacity is determined by the area of the surface bounding a volume and not by the volume.
Try to imagine possible mechanisms by which the states of Planckons submerged in the bulk could be accessed, i.e., read or written. Any such infrastructure and mechanism for implementing such read or write operations would have to reside in the bulk. E.g., perhaps one might imagine some internal system of say, 1-Planckon thick, buses threading through the bulk, providing access to those submerged Planckons. Thus, some of the 512 bulk Planckons cannot be available for storing information. While this would reduce the information storage limit to something less than the full volume in Planck volumes, it does not explain why it should be reduced all the way down to being approximately equal the number of Planckons comprising the 2D boundary.
Rather than address the 3D case directly, let’s reduce the dimension of the problem by one. Accordingly, Fig. 4 shows a 2D space, a 2D bulk, the 5×5 array of rose Planckons, wrapped by a 1D boundary, comprised of 20 white Planckons. The analogy of the 3D version of the holographic principle would predict that the amount of information that can be stored in the 25 Planckon (25 bit) bulk equals the amount of information that can be stored in the 20 Planckon boundary, again, disregarding the divisor of four.
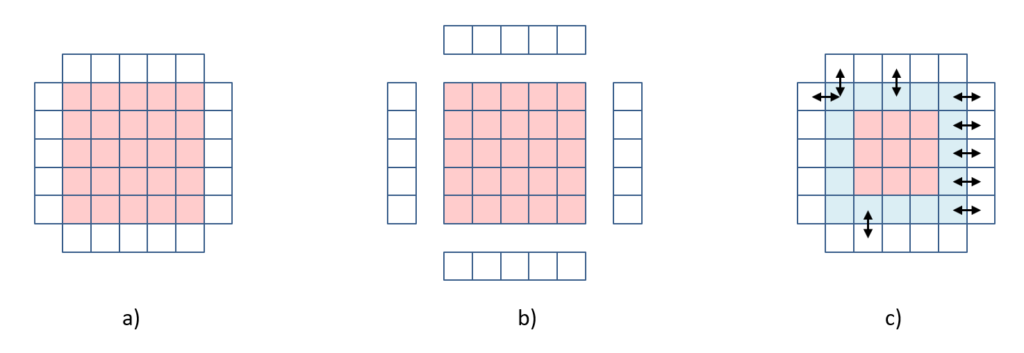
Since we assume that physical effects can only be transmitted through edge connections (not corners), only the 16 bulk Planckons comprising the outermost, one-Planckon-thick shell of the bulk (blue Planckons) are directly accessible from the boundary (arrows show examples of access paths). We can imagine those 16 bulk Planckons, as a memory of bits just as in a regular computer memory and the Planckons comprising the boundary (perhaps along with additional Planckons extending into the space beyond the boundary) to be a bus, or connection matrix, for accessing (writing or reading) these 16 bits. In any case, the innermost nine Planckons of the bulk (rose Planckons in Fig. 4c) are not directly accessible from the boundary. We then have the question as to how the states of those innermost nine bulk Planckons could help to increase the storage capacity of the bulk.
Rather than attempt to construct such an infrastructure and (read and write) operations, let’s instead imagine how submerged Planckons might be able to be seen through other Planckons, and thus possibly affect the state of the (one or more) boundary Planckons. We can actually make the problem easier, and without loss of generality, by reducing the problem by one dimension.
The answer is that they cannot increase the storage capacity. Why?
It seems there are two approaches
- We can treat the bulk as a cellular automata in which case we define a rule by which a Planckon updates its states as a function of its own state and those of its four edge-adjacent neighbors. In this case, there is only one rule, which operates in every Planckon. In particular, this means all Planckons are of the same type.
- We can treat consider the bulk’s Planckons as being of two types: a) ones that hold a binary state, i.e., bits of memory, as we have already postulated for the outermost 16 Planckons of the bulk; and b) ones that implement communication, i.e., transmit signals, in which case, we’re allowing that the communication infrastructure (bus, matrix) now extends into the bulk itself.
In the first approach, for there to be a positive answer to the challenge question, there must be an update rule (i.e. dynamics) which allows 25 bits to be stored and retrieved. In the second approach, where we partition the bulk’s Planckons into two disjoint subsets, those that hold state, which we will call a memory, or a coding field, and those that transmit signals, we need to define the structure (topology) of both parts, the coding field and the signal transmission partition.
…STILL BEING WRITTEN…
So it seems that we are led to the concept of a corpuscle of space. As defined elsewhere, the corpuscle is the smallest completely connected region of space, i.e., where the coding field Planckons are completely connected to themselves (a recurrent connection) and completely connected to the Planckons comprising the corpuscle’s boundary. So in this case, the model is explicitly not a cellular automata, where the physical units tiling a space are connected only to nearest neighbors according to the dimension of the space in which the physical units exist. Rather, by assigning some Planckons to be for communication and some for states, we make possible connectivity schemes that are not limited to the underlying space’s dimension, but rather can allow arbitrarily higher dimensionality (topology) for subset of Planckons devoted to representing state.
So it’s just as simple as that. If space is discrete, then the amount of information that can be contained in a 3D volume equals the amount of information that can be contained in its 2D (though actually, one-Planckon thick) boundary. Also, note that the argument remains qualitatively the same if we consider the bulk and boundaries as spheres instead.
There are only 2384 possible messages (signals) we could receive from this bulk. So even though there are vastly more , i.e., 2512, unique states of the bulk, all of those states necessarily fall into only 2384 equivalence classes. And similarly, there are only 2384 messages we could send into the bulk, meaning that all possible states of the vastly larger world outside the bulk similarly fall into only 2384 equivalence classes. No matter what computational process we can imagine that operates inside the bulk, i.e., no matter which of it’s 2384 states is produced by such process, and furthermore, no matter how many steps the process producing that state takes, it can only produce 2384 output messages.
A well-known quantum computation theorist told me that the above is simply a re-statement of the holographic principle, not an explanation. In particular, he said that I need to explain why we could not send more than 384, or in fact, all 512 bits of information into the bulk by sending multiple messages. So here is the explanation of why multiple messages doesn’t help.