If concepts are represented localistically, the first, the most straightforward thing to do is to place those representations in an external coordinate system (of however many dimensions as desired/needed).  The reason is that localist representations of concepts have the semantics of “point masses”.  They have no internal structure and no extension.  So it is natural to view them as points in an N-dimensional coordinate system.  You can then measure the similarity of two concepts (points) using for example, Euclidean distance.  But, note that placing a new point in that N-space does not automatically compute and store the distance between that new point and ALL points already stored in that N-space.  This requires explicit computation and therefore expenditure of time and power.

On the other hand, if concepts are represented using sparse distributed codes (SDCs), i.e., sets of co-active units chosen from a much larger total field of units, where the sets may intersect to arbitrary degrees, then it becomes possible to measure similarity (inverse distance) as the size of intersection between codes.  Note that in this case, the representations (the SDCs) fundamentally have extension…they are not formally equivalent to point masses.  Thus, there is no longer any need for an external coordinate system to hold these representations.  A similarity metric is automatically imposed on the set of represented concepts by the patterns of intersections of their codes.  I’ll call this an internal similarity metric.

Crucially, unlike the case for localist codes, creating a new SDC code (i.e., choosing a set of units to represent a new concept), DOES compute and store the similarities of the new concept to ALL stored concepts.  No explicit computation, and thus no additional computational time or power, is needed beyond the act of choosing/storing the SDC itself.

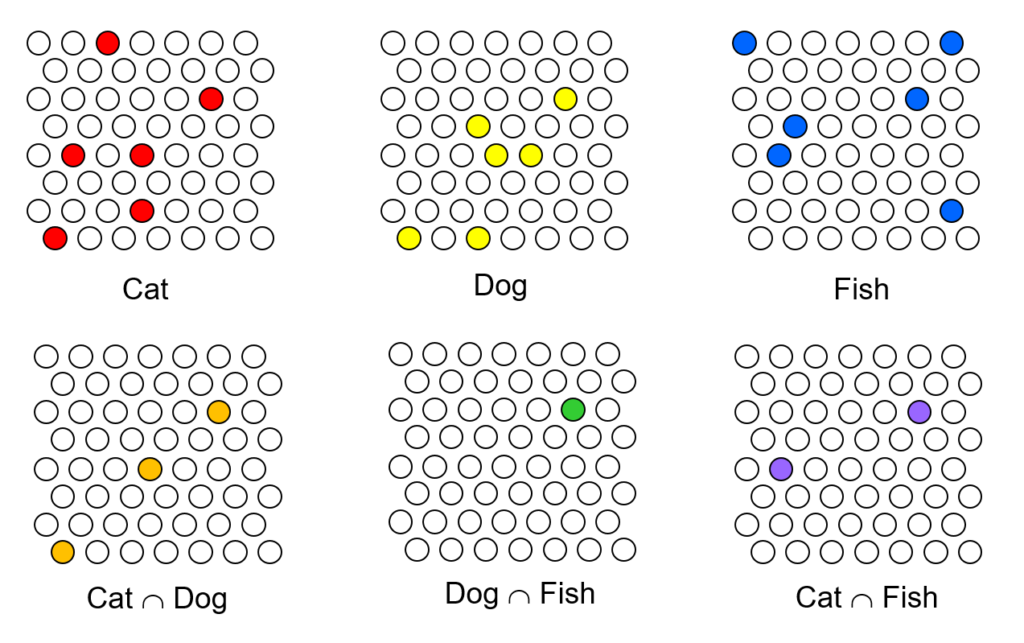
Consider the toy example below.  Here, the format is that all codes will consist of exactly 6 units chosen from the field.  Suppose the system has assigned the set of red cells to be the code for the concept, “Cat”.  If the system then assigns the yellow cells to be the code for “Dog”, then in the act of choosing those cells, the fact that three of the units (orange) are shared by the code for “Cat” implicitly represents (reifies in structure) a particular similarity measure of “cat” and “Dog”.  If the system later assigns the blue cells to represent “Fish”, then in so doing, it simultaneously reifies in structure particular measures of similarity to both “Cat” and “Dog”, or in general, to ALL concepts previously stored.  No additional computation was done, beyond the choosing of the codes themselves, in order to embed ALL similarity relations, not just the pairwise ones, but those of all orders (though this example is really too small to show that), in the memory.

This is why I talk about SDC as the coming revolution in computation. Computing the similarities of things is in some sense the essential operation that intelligent computers perform.  Twenty years ago, I demonstrated, in the form of the constructive proof that is my model TEMECOR, now Sparsey®, that choosing an SDC for a new input, which respects the similarity structure of the input space, can be done in fixed time (i.e., the number of steps, thus the compute time and power, remains constant as additional items are added).  In light of the above example, this implies that an SDC system computes an exponential number of similarity relations (of all orders) and reifies them in structure also in fixed-time.

Now, what about the possibility of using localist codes, but not simply placed in an N-space, but stored in a tree structure?  Yes.  This is, I would think, essentially how all modern databases are designed.  The underlying information, the fields of the records, are stored in localist fashion, and some number E of external tree indexes are constructed and point into the records.  Each individual tree index allows finding the best-matching item in the database in log time, but only with respect to the particular query represented by that index.  When a new item is added to the database all E indexes must execute their insertion operations independently.  In the terms used above, each index computes the similarity relations of a new item to ALL N stored items and reifies them using only logN comparisons.  However, the similarities are only those specific to the manifold (subspace) corresponding to index (query).  The total number of similarity relations computed is the sum across the E indexes, as opposed to the product. But it is not this sheer quantitative difference, but rather that having predefined indexes precludes reification of almost all of the similarity relations that in fact may exist and be relevant in the input space.

Thus I claim that SDC admits computing similarity relations exponentially more efficiently than localist coding, even localist codes augmented by external tree indexes.  And, that’s at the heart of why in the future, all intelligent computation will be physically realized via SDC….and why that computation will be able to be done as quickly and power-efficiently as in the brain.