Category Archives: Uncategorized

A Simple explanation of the Holographic Principle

Uncategorized

The holographic principle says that the maximum amount of information that can be contained in a volume (bulk) is upper-bounded by the amount of information that can be contained on the surface (boundary) of that bulk. On first thought, this seems absurd: common sense tells us that there is so much more matter comprising a bulk than comprising its surface. But here I give a simple argument why the boundary is the limiting factor. The argument relies on several assumptions.

  1. Space is discrete
  2. There is a smallest volume of space
  3. Space is a cubic tiling at that smallest scale
  4. those smallest volumes (cubes) are binary-valued
  5. Time is discrete
  6. messages (signals) can only be sent locally, i.e., to an immediately neighboring cube.

So here’s the argument.

The apparent (emergent) universe we inhabit has three macroscopic spatial dimensions.  The theoretical smallest length (distance) is one Planck length.  So let’s assume that space is a 3D cubic tiling of volumes, i.e., cubes, one Planck length on a side, as in Fig. 1. I call them “planckons“. But note that despite the ending “ons”, these are not particles like those of the Standard Model (SM). In particular, they do not move: they are the units of space itself. Because they are so small and because they can’t have any internal structure, let’s assume that they are binary.  Either matter exists in a cube or it’s empty, i.e., either a planckon exists (“1”), or it does not (“0”).  Planckons have no other properties, e.g., spin, charge.  Functionally, they are just bits.

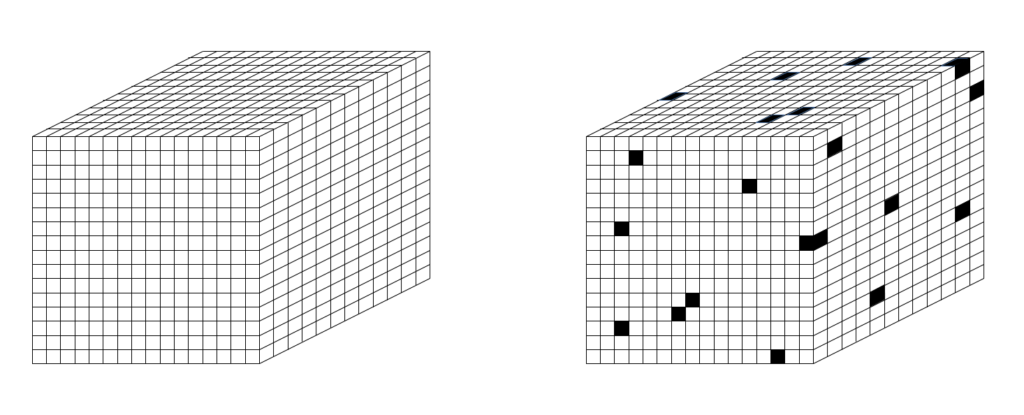
Fig. 1: Space is a 3D tiling of Planck-size cubes. These “planckons” are binary-valued.

Now consider a cube of space, C, e.g., 8 Planck lengths on a side, as in Fig. 2.  C is a bulk.  C contains 512 planckons.  Since they are binary, there are 2512 possible states of C.  So, C can contain 512 bits of information. Now consider a layer of planckons that just wraps C. It consists of 6 x 64 = 384 planckons.  That 1-Planck-cube-thick layer is the boundary, B, between C and the rest of the universe, U. It constitutes a communication channel between C and U. But B consists of only 384 planckons, so it has only 2384 states and so B can contain at most 384 bits. 

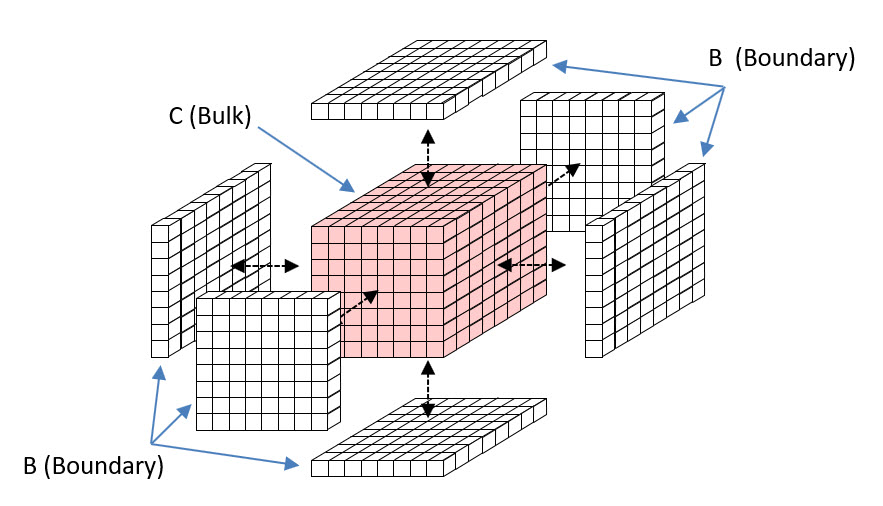
Fig.2: Depiction of a 3D bulk, C, consisting of 8x8x8=512 binary planckons and its boundary, B, that is the union of the six 8×8 2D arrays of planckons, for a total of 384 planckons, that wraps the bulk.

Suppose that a particular state (pattern), X, over the 512 bits (out of the 2512 possible patterns) exists. Now think of reading out the contents of C. That must occur as some instantaneous pattern over B’s 384 bits. So, no matter what actual pattern over C’s 512 bits actually exists, we can only read (at most) 384 bits from C. And similarly, we can only store at most 384 bits into C.

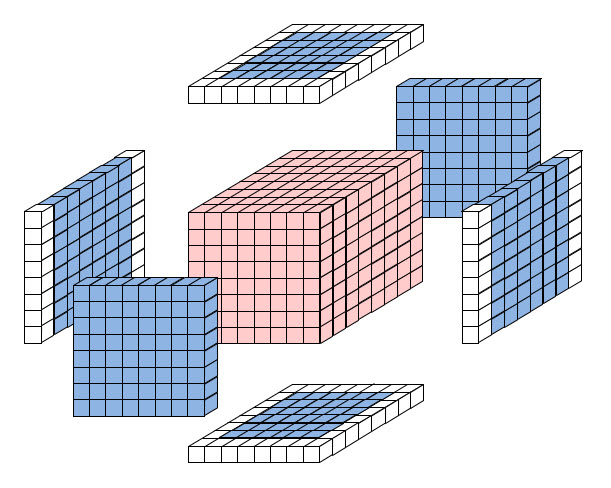
You might attempt to challenge my assertion that any read-out (or read-in) must be instantaneous. Why can’t we consider messages that take two (or more) time steps to send across the boundary (channel)? For example, suppose we imagine the cubes comprising B to be made of glass, so that you would just see the bit of C (the bulk) that is directly “under” the adjacent bit of B (the boundary), as in Fig. 3. There are 296 bits comprising the bulk’s outer layer: these are the rose-colored cubes. These could be seen through, i.e., copied to, B. But, how would any of the more deeply submerged cubes of the bulk be “seen” at B? You might imagine some temporal process by which the submerged bits of the bulk could be brought up next to the boundary. But the physical instantiation of any such “surfacing” process would require physical substrate. But, all 512 cubes (the totality of the bulk), is already accounted for in the pattern, X, itself. There are no additional bits available to build any such surfacing process (algorithm). So, we’re left with the conclusion that the amount of information that can be “seen in”, or extracted from, this bulk is upper-bounded by the number of bits comprising the boundary, i.e., the holographic principle. One cannot simply assume a physical, sequential process, allowing some kind of “surfacing” to read out the 512 – 296 = 216 submerged bits. One would have to describe the physical embodiment of any such process, and again, we’ve already used up all the bits in calculating the amount of information contained in the bulk.

Fig. 3: Blue regions of boundary portions show one way of uniquely associating the bulk’s 296 outer layer bits (rose-colored) with boundary bits, so as to avoid double-counting (due to some of those bulk bits facing two or more boundary bits).

I suppose we could consider allocating some fraction of the bulk’s 512 bits to representing that surfacing procedure. That’s worth exploring. But Bekenstein, Hawking, ‘t Hooft, and others have already shown that the amount of the information storable in a black hole (the densest possible bulk) is a 1/4 the area of its surface in Planck units, which is already several times lower than my simple argument would allow. This suggests finding such a partitioning, and accompanying description of the embodiment/operation of the surfacing algorithm, would be unlikely.

Conclusion

The pure concept of the holographic principle is that the maximum amount of information that can be stored in a volume is less than or equal to the amount of information that can be stored on its surface. This is highly counterintuitive. Indeed it is simply inconsistent with our everyday, macroscopic experience. But by making a few simple assumptions about the nature of the physical world, most importantly, that at the smallest scale, space itself is discrete, that units of space of this smallest size are binary, and that signaling is local, I construct a simple, classical explanation of why the holographic principle must be true.

Indeed, it’s a very simple argument. It does not require require the formalisms of quantum field theory (QFT) or string theory. But I have it on good authority that simpler explanations are better than more complicated ones 🙂 Some physicists have proposed the possibility that in the end, everything, i.e., this entire apparent (emergent) universe and all that happens in it, is just information, cf. Wheeler’s “It from Bit”. If so, then arguments like mine, or more generally, models in which states are ultimately just bit patterns and dynamics is just computational operations performed on bits, should be expected.

Learned Multidimensional Indexes

Uncategorized

At the ends of papers and talks on the “learned indexes” concept described by Kraska et al in 2017, an exciting future research direction referred to as “multidimensional indexes” is suggested.

I described a multidimensional index concept about 10 years ago (unpublished) but referred to it as learning representations that were “simultaneously physically ordered on multiple uncorrelated dimensions”. The crucial property that allows informational items, e.g., records of a database consisting of multiple fields (dimensions, features), to be simultaneously ordered on multiple dimensions is that they have the semantics of extended bodies, as opposed to point masses.  Formally, this means that items must be represented as sets, not vectors.

Why is this? Fig. 1 gives the immediate intuition. Let there be a coding field consisting of 12 binary units and let the representation, or code, which we will denote with Greek letter φ, of an item be a subset consisting of 5 of the 12 units.  First consider Fig. 1a.  It shows a case where three inputs, X, Y, and Z, have been stored.  To the right of the codes, we show the pairwise intersections of the three codes.  In this possible world, PW1, the code of X is more similar to the code of Y than to that of Z.  We have not shown you the specific inputs and we have not described the learning process that mapped these inputs to these codes.  But, we do assume that that learning process preserves similarity, i.e., it maps more similar input to more highly intersecting codes.  Given this assumption, we know that

sim(X,Y) > sim(X,Z) and also that sim(Y,Z) > sim(X,Z).

PW1_PW2_XYZ_ordering

Fig. 1

That is, this particular pattern of code intersections imposes constraints on the statistical (and thus, physical) structure of PW1.  Thus, we have some partial ordering information over the items of PW1. We don’t know the nature of the physical dimensions that have led to this pattern of code intersections (since we haven’t shown you the inputs or the input space).  We only know that there are physical dimensions on which items in PW1 can vary and that that X, Y, and Z have the relative similarities, relative orders, given above.  But note that given only what has been said so far, we could attach names to these underlying physical dimensions (regardless of what they actually are).  That is, there is some dimension of the input space on which Y is more similar to X than is Z.  Thus, we could call this dimension, “X-ness”.  Y has more X-ness than Z does.  Similarly, there is another physical dimension present that we can call “Y-ness”, and Z has more Y-ness than X does.  Or, we could label that dimension “Z-ness”, in which case, we’d say that Y has more Z-ness than X does.

Now, consider Fig 1b.  It shows an alternative set of codes for X, Y and Z, that would result if the world had a slightly different physical structure.  Actually, the only change is that Y has a slightly different code.  Thus, the only difference between PW2 and PW1 is that in PW2, whatever physical dimension X-ness corresponds to, item Y has more of it than it does in PW1. That’s because |{φ(X) ∩ φ(Y)| = 3 in PW2, but equals 2 in PW1. ALL other pairwise relations are the same in PW2 as they are in PW1.  Thus, what this example shows, is that the representation has the degrees of freedom to allow ordering relations on one dimension to vary without impacting orderings on other dimensions. While it is true that this is a small example, I hope it is clear that this principle will scale to higher dimensions and much larger numbers of items.  Essentially, the principle elaborated here leverages the combinatorial space of set intersections (and intersections of intersections, etc.) to counteract the curse of dimensionality.

The example of Fig. 1 shows that when items are represented as sets, they have the internal degrees of freedom to allow their degrees of physical similarity on one dimension to be varied while maintaining their degrees of similarity on another dimension.  We actually made a somewhat stronger claim at the outset, i.e., that items represented as sets can simultaneously exist in physical order on multiple uncorrelated dimensions.  Fig. 2 shows this directly, for the case where the items are in fact simultaneously ordered on two completely anti-correlated dimensions.  

In Fig. 2, the coding field consists of 32 binary units and the convention is that all codes stored in the field will consist of exactly 8 active units. We show the codes of four items (entities), A to D, which we have handpicked to have a particular intersection structure.  The dashed line shows that the units can be divided into two disjoint subsets, each representing a different “feature” (latent variable) of the input space, e.g., Height (H) and IQ (Q).    Thus, as the rest of the figure shows, the pattern of code intersections simultaneously represents both the order, A > B > C > D, for Height and the anti-correlated order, D > C > B > A, for IQ.

simple_simul_order_two_fields_anticorr

Fig. 2

The units comprising this coding field may generally be connected, via weight matrices, to any number of other, downstream coding fields, which could “read out” different functions of this source field, e.g., access the ordering information on either of the two sub-fields, H or Q.

The point of these examples is simply to show that a set of extended objects, i.e., sets, can simultaneously be ordered on multiple uncorrelated dimensions.  But there are other key points including the following.

  1. Although we hand-picked the codes for these examples, the model, Sparsey, which is founded on using a particular format of fixed-size sparse distributed representation (SDR), and which gave rise to the realization described in this essay, is a single-trial, unsupervised learning model that allows the ordering (similarity) relations on multiple latent variables to emerge automatically.  Sparsey is described in detail in several publications: 1996 thesis, 2010, 2014, 2017 arxiv.
  2. While conventional, localist DBs use external indexes (typically trees, e.g., B-trees, KD-trees) to realize log time best-match retrieval, the set-based representational framework described here actually allows fixed-time (no serial search) approximate best-match retrieval on the multiple, uncorrelated dimensions (as well as allowing fixed-time insertion).  And, crucially, there are no external indexes: all the “indexing” information is internal to the representations of the items themselves.  In other words, there is no need for these set objects to exist in an external coordinate system in order for the similarity/ordering relations to be represented and used.

Finally, I underscore two major corollary realizations that bear heavily on understanding the most expedient way forward in developing “learned indexes”.

  1. A localist representation cannot be simultaneously ordered on more than one dimension.  That’s because localist representations have point mass semantics.  All commercial DBs are localist: the records of a DB are stored physically disjointly.  True, records may generally have fields pointing to other records, which can therefore be physically shared by multiple records.  But any record must have at least some portion that is physically disjoint from all other records.  The existence of that portion implies point mass semantics and (ignoring the trivial case where two or more fields of the records of a DB are completely correlated) a set of points can be simultaneously ordered (arranged) on at most one dimension at a time.  This is why a conventional DB generally needs a unique external index (typically some kind of tree structure) for each dimension or tuple on which the records need to be ordered so as to allow fast, i.e., log time, best-match retrieval.
  2. In fact, dense distributed representations (DDR), e.g., vectors of reals, as for example present in the internal fields of most mainstream machine learning / deep learning models, also formally have point mass semantics.  Intersection is formally undefined for vectors over reals.  Thus, any similarity measure between vectors (points) must also formally have point mass semantics, e.g., Euclidean distance.  Consequently, DDR also  precludes simultaneous ordering on multiple uncorrelated dimensions.

Fig. 3 gives final example showing the relation of viewing items in terms of a point representation to set representation.  Here the three stored items are purple, blue, and green.  Fig. 3a begins showing the three items as points with no internal structure sitting in a vector space and having some particular similarity (distance) relationships, namely that purple and blue are close and they are both  far away from green.  In Fig. 3b, we now have set representations of the three items.  There is one coding field here, consisting of 6×7=42 binary units and red units show intersection with the purple item’s representation. Fig 3c shows that the external coordinate system is no longer needed to represent the similarity (distance) relationships, and Fig. 3d just reinforces the fact that there is really only one coding field here and that the three codes are just different activation patterns over that single field. The change from representing information formally as points in an external space to representing them as sets (extended bodies) that require no external space will revolutionize AI / ML.

stepwise_explan_vec_space_to_sets

 Fig. 3

Not Copenhagen, Not Everett, a New Interpretation of Quantum Reality

Uncategorized, , , , , , ,

I’ve claimed for some time that quantum computing can be realized on a single processor Von Neumann machine and published a paper explaining the basic intuition. All that is necessary is to represent information using sparse distributed codes (SDC) rather than localist codes. With SDC, all informational states (hypotheses) represented in a system (e.g., computer) are represented in physical superposition and therefore all such states are partially active in proportion to their similarity with the current most likely (most active) state. My Sparsey® system operates directly on superpositions, transforming the superposition over hypotheses at T into the superposition at T+1 in time that does not depend on the number of hypotheses represented (stored) in the system. This update occurs via passage of signals via a recurrent channel, i.e., a recurrent weight matrix. In addition to a serial (in time) updating of the superposition, mediated by the recurrent matrix, the system may also have an output channel (a different, non-recurrent weight matrix) that “taps” off, i.e., observes, the superposition at each T. Thus the system can generate a sequence of collapsed outputs (observations) which can be thought of as a sequence of maximum likelihood estimates, as well as continuously update the superposition (without requiring collapse).

This has led me to the following interpretation of the quantum theory of the physical universe itself.  Projecting a universe of objects in a low dimensional space, e.g., 3 dimensions, up into higher dimensional spaces, causes the average distance between objects to increase exponentially with the number of dimensions. (The same is true of sparse distributed codes living in a sparse distributed code space.) But now imagine that the objects in the low dimensional space are not point masses, but rather have extension. Specifically, let’s imagine that these objects are something like ball-and-stick lattices, or 3D graphs consisting of edges and nodes. The graph has extension in 3 dimensions, but is mostly just space.  Further, imagine that the graph edges simply represent forces between the nodes (and not constrained to be pairwise forces), where the nodes are the actual material constituents of objects (similar to how an atom is mostly space…and perhaps even a proton is mostly empty space).

Now suppose that the actual universe is of huge dimension, e.g., a million dimensions, or an Avogadro’s number of dimensions, but let’s stick with one million for simplicity. Furthermore, imagine that these are all macroscopic dimensions (as opposed to the Planck-scale rolled up dimensions of string theory). Now imagine that this million-D universe is filled with macroscopic “graph” objects.  They would have macroscopic extent on perhaps a large fraction or even all of those 1 million dimensions, but they would be almost infinitely sparse or diffuse, i.e., ghost-like, so diffuse that numerous, perhaps exponentially numerous such objects, could exist in physical superposition with each other, i.e., physically intermingled.  They could easily pass through each other.  But, as they did so, they would physically interact.

Suppose that we can consider two graphs to be similar in proportion to how many nodes they share in common. Thus two graphs that had a high fraction of their nodes in common might represent two similar states of the same object.

But suppose that instead of thinking of a single graph as representing a single object, we think of it as representing a collection of objects.  In this case, two graphs having a certain set of nodes in common (intersection), could be considered to represent similar world states in which some of the same objects are present and perhaps where some of the those objects have similar internal states and some of the inter-object relations are similar.  Suppose that such a graph, S, consisted of a very large number (e.g., millions) of nodes and that a tiny subset, for concreteness, say, 1000, of those nodes corresponded to the presence of some particular object x.  Then imagine another instance of the overall graph, S’, in which 990 of those nodes are present.  We could imagine that that might represent another state of reality in which x manifests almost identically as it did in the original instance; call that version of x, x‘.  Thus, if S was present, and thus if x was present, we could say that x‘ is also physically present, just with 990/1000 strength rather than with full strength.  In other words, the two states of reality can be said to be physically present, just with varying strength.  Clearly, there are an exponential number of states around x that could also be said to be partially physically present.

Thus we can imagine that the actual physical reality that we experience at each instant is a physical superposition of an exponentially large number of possible states, where that superposition, or world state, corresponds to an extremely diffuse graph, consisting of a very large number of nodes, living in a universe of vastly high dimension.

This constitutes a fundamentally new interpretation of physical reality in which, in contrast to Hugh Everett’s “many worlds” theory, there is only one universe.  In this single universe, objects do physically interact via all the physical forces we already know of.  It’s just that the space itself has such high dimension and these object’s constituents are so diffuse that they can simply exist on top of each other, pass through each other, etc.  Hence, we have found a way for actual physical superposition to be the physical realization of quantum superposition.

Imagine projecting this 1 million dimensional space down into 3 dimensions. These “object-graphs”, which are exponentially diffuse in the original space, will appear dense in the low dimensional manifold. Specifically, the density of such objects increases exponentially with decreasing number of dimensions. I submit that what we experience (perceive) as physical reality is simply an extremely low dimensional, e.g. 3 or 4 dimensions, projection of a hugely-high dimensional universe, whose objects are macroscopic but extremely diffuse.  Note that these graphs (or arbitrary portions thereof) can have rigid structure (due to the forces amongst the nodes).

In particular, this new theory obviates the need for the exponentially large number of physically separate universes that Everett’s theory requires.  Any human easily understands the massive increase in space in going from 1-D to 2-D or from 2-D to 3-D.  There is nothing esoteric or spooky about it.  Anyone can also understand how this generalizes to adding an arbitrary number of dimensions.  In contrast, I submit that no human, including Everett, could offer a coherent explanation of what it means to have multiple, physically separate universes.  We already have the concept, which we are all easily taught in childhood, that the “universe” is all there is.  There is no Physical room for any additional universes.  The “multiverse”—a hypothesized huge or infinite set of physical universes—is simply an abuse of language.

Copenhagen maintains that all possible physical states exist in superposition at once and that when we observe reality, that superposition collapses to one state. But Copenhagen never provided an intuitive physical explanation for this quantum superposition.  What Copenhagen simply does not explain, and what Everett solves by positing an exponential number of physically separate, low-dimensional universes, filled with dense, low-D objects, I solve by positing a single super-high dimensional universe filled with super-diffuse, high-D objects.

Slightly as an aside, this new theory helps resolve a problem I’ve always had with Schrodinger’s cat.  The two states, “cat alive” and “cat dead” are constructed to seem very different.  This misleads people into thinking that at every instant and in every physical subsystem, a veritable infinity of states coexist in superposition.  I mean…why stop at just “cat alive” and “cat dead”?  What about the state in which a toaster has appeared, or a small nuclear-powered satellite?  I suppose it is possible that some vortex of physical forces, perhaps designed by a supercomputer, could instantly rearrange all the atoms in the box from one in which there was a live cat to one in which there is the toaster, or the satellite.  But I think it is better to think of transformations like this to have zero probability.  My point here is that the number of physical states to which any physical subsystem might collapse at any given moment, i.e., the cardinality of the superposition that exists at that moment, is actually vastly smaller than one might naively think having been misled by the typical exposition of Schrodinger’s cat.  Thus, it perhaps becomes more plausible that my theory can accommodate the number of physical states that actually do coexist in superposition.

Again, this theory of what physical reality actually is came to me by first understanding and constructing a similar theory of information representation and processing in the brain, i.e., a theory about representing items of information, not actual physical entities.  In that SDC theory, the universe is a high-D “codespace”, the “objects” are “representations” or “codes”, and these codes are high-D but are extremely diffuse (sparse) in that codespace.

Sparse distributed representations compute similarity relations exponentially more efficiently than localist representations

Uncategorized, ,

If concepts are represented localistically, the first, the most straightforward thing to do is to place those representations in an external coordinate system (of however many dimensions as desired/needed).  The reason is that localist representations of concepts have the semantics of “point masses”.  They have no internal structure and no extension.  So it is natural to view them as points in an N-dimensional coordinate system.  You can then measure the similarity of two concepts (points) using for example, Euclidean distance.  But, note that placing a new point in that N-space does not automatically compute and store the distance between that new point and ALL points already stored in that N-space.  This requires explicit computation and therefore expenditure of time and power.

On the other hand, if concepts are represented using sparse distributed codes (SDCs), i.e., sets of co-active units chosen from a much larger total field of units, where the sets may intersect to arbitrary degrees, then it becomes possible to measure similarity (inverse distance) as the size of intersection between codes.  Note that in this case, the representations (the SDCs) fundamentally have extension…they are not formally equivalent to point masses.  Thus, there is no longer any need for an external coordinate system to hold these representations.  A similarity metric is automatically imposed on the set of represented concepts by the patterns of intersections of their codes.  I’ll call this an internal similarity metric.

Crucially, unlike the case for localist codes, creating a new SDC code (i.e., choosing a set of units to represent a new concept), DOES compute and store the similarities of the new concept to ALL stored concepts.  No explicit computation, and thus no additional computational time or power, is needed beyond the act of choosing/storing the SDC itself.

Consider the toy example below.  Here, the format is that all codes will consist of exactly 6 units chosen from the field.  Suppose the system has assigned the set of red cells to be the code for the concept, “Cat”.  If the system then assigns the yellow cells to be the code for “Dog”, then in the act of choosing those cells, the fact that three of the units (orange) are shared by the code for “Cat” implicitly represents (reifies in structure) a particular similarity measure of “cat” and “Dog”.  If the system later assigns the blue cells to represent “Fish”, then in so doing, it simultaneously reifies in structure particular measures of similarity to both “Cat” and “Dog”, or in general, to ALL concepts previously stored.  No additional computation was done, beyond the choosing of the codes themselves, in order to embed ALL similarity relations, not just the pairwise ones, but those of all orders (though this example is really too small to show that), in the memory.

This is why I talk about SDC as the coming revolution in computation. Computing the similarities of things is in some sense the essential operation that intelligent computers perform.  Twenty years ago, I demonstrated, in the form of the constructive proof that is my model TEMECOR, now Sparsey®, that choosing an SDC for a new input, which respects the similarity structure of the input space, can be done in fixed time (i.e., the number of steps, thus the compute time and power, remains constant as additional items are added).  In light of the above example, this implies that an SDC system computes an exponential number of similarity relations (of all orders) and reifies them in structure also in fixed-time.

Now, what about the possibility of using localist codes, but not simply placed in an N-space, but stored in a tree structure?  Yes.  This is, I would think, essentially how all modern databases are designed.  The underlying information, the fields of the records, are stored in localist fashion, and some number E of external tree indexes are constructed and point into the records.  Each individual tree index allows finding the best-matching item in the database in log time, but only with respect to the particular query represented by that index.  When a new item is added to the database all E indexes must execute their insertion operations independently.  In the terms used above, each index computes the similarity relations of a new item to ALL N stored items and reifies them using only logN comparisons.  However, the similarities are only those specific to the manifold (subspace) corresponding to index (query).  The total number of similarity relations computed is the sum across the E indexes, as opposed to the product. But it is not this sheer quantitative difference, but rather that having predefined indexes precludes reification of almost all of the similarity relations that in fact may exist and be relevant in the input space.

Thus I claim that SDC admits computing similarity relations exponentially more efficiently than localist coding, even localist codes augmented by external tree indexes.  And, that’s at the heart of why in the future, all intelligent computation will be physically realized via SDC….and why that computation will be able to be done as quickly and power-efficiently as in the brain.