Category Archives: quantum foundations

A Set-based Quantum Theory

Hyperdimensional Computing, Quantum Computing, quantum foundations, Sparse Distributed Representations, , , , , , ,

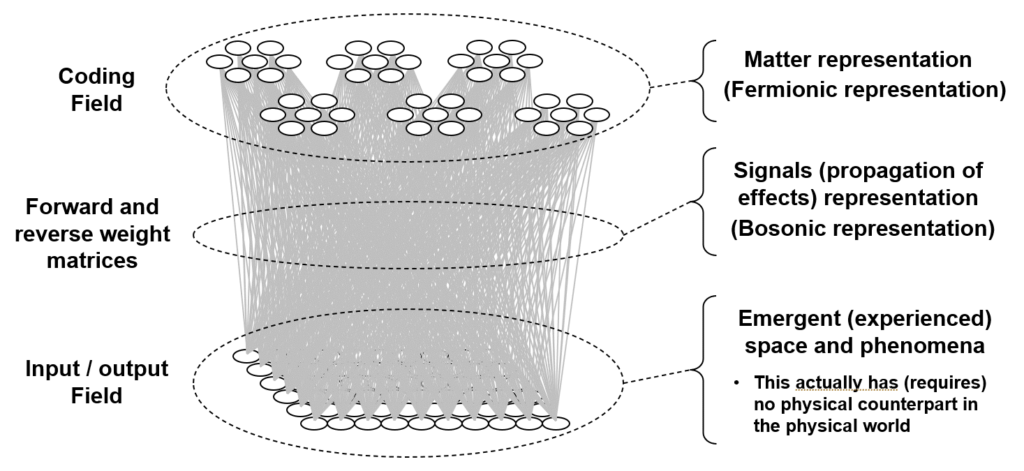
Quantum theory (QT) is based on vectors. In QT, the physical system (world) is represented as an infinite-dimensional Hilbert space. The space is ontologically prior to the stuff, i.e., matter and energy, or fields if you like, that exists in the space.  Each state of the system is defined as a point in the Hilbert space. Thus, the space of QT, i.e., the Hilbert space itself, is definitely not emergent. In the theory I describe here, there is also something that exists prior to the stuff. But it is not a vector (tensor) space. It’s just a set, a collection of unordered elements. These elements are the simplest possible, just binary elements (bits) that can be active (“1”) or inactive (“0”).  Instead of the states being defined as points in a space, they are defined as subsets, very sparse subsets, of the overall, or universal, set. More precisely, I will define the matter (fermionic) states of the physical system as these sparse subsets. Thus, I will call this universal set the fermionic field.  My theory will be able to explain the existence of individual matter entities (fermions) moving and interacting in lawful ways but these entities and the space within which they apparently move/interact will be emergent, i.e., epiphenomenal. In fact, any one dimension of the emergent space will be explained as the combination of: a) a pattern of intersections that exists over the sets that define the fermionic states of the system; and b) the sequential patterns of activation of those intersections through time.

In addition to the fermionic field, my theory also has a complete recurrent matrix of binary-valued connections, or weights, from the set of bits comprising the fermionic field back to itself.  It is this matrix that mediates all changes of state from one time step to the next, i.e., the system’s dynamics.  In other words, it is the medium by which effects, or signals, propagate.  Thus, I call it the bosonic field. Note that my theory’s mechanics, i.e., the operation (algorithm) that executes the dynamics, is simpler, more fundamental, than any particular force of the standard model (SM).  My theory has the capacity to explain, i.e., mechanistically represent, any force, i.e. any lawful pattern of changes of state through time.  In fact, any such force will also be emergent: as suggested above, the fermionic evidence of any instance of the application of any force will be physically reified as a temporal sequence of activations of intersections. And the actual physical reification of the force at any given moment is the set of signals traversing the matrix from the set of active fermionic bits at t (which arrive back at the matrix at t+1). Thus, in this theory, nothing actually moves. That is, neither the fermionic nor the bosonic bits move. They change state, i.e., activate or deactivate, but they don’t move. All apparent motion of higher-level, e.g., standard model (SM) level, fermions and bosons, is explained as these patterns of activation/deactivation. We’re all very familiar with this concept. When you watch TV and see all the things moving/interacting, none of the pixels are actually moving. They’re just changing state.

As will become apparent, in my theory, the underlying problem is: can we find a set of state-representing sets and a setting of the matrix’s weights that implement (simulate) any particular emergent world, i.e., any given emergent space, in general, having multiple dimensions, some of which are spatial and some not, and multiple fermionic entities? This can be viewed as a search problem through the combinatorially large space of possible sets of state-representing sets and weight sets. The way I’ll proceed in describing this theory is by construction. I’ll choose a particular set of state-representing sets.  I’ll choose them so that they have a particular pattern of monotonically decreasing intersections.  Thus, that pattern of intersections constitutes a representation of a similarity (inverse distance) relation over the states. I’ll then show that there is a setting of the weights of the matrix, which, together with an algorithm (operator) for changing/updating the state, constrains the states to activate in a certain order, namely an order that directly correlates with the intersection sizes. Thus, the operator enforces gradual change through time of the value of that similarity (inverse distance) measure, i.e., it enforces locality (local realism) in the emergent space.

The Set-Based Theory

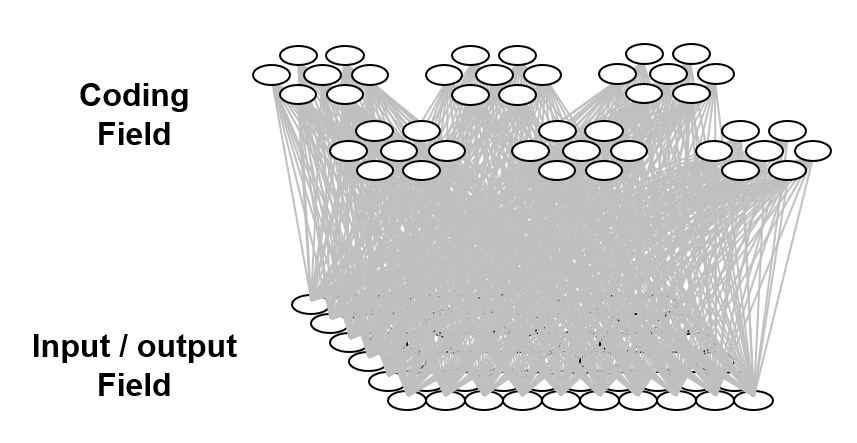
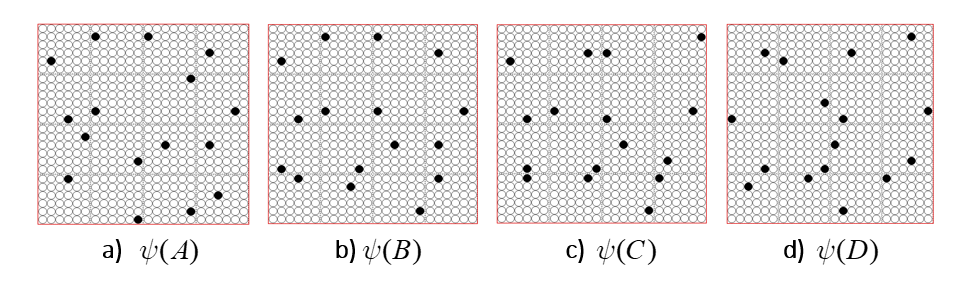
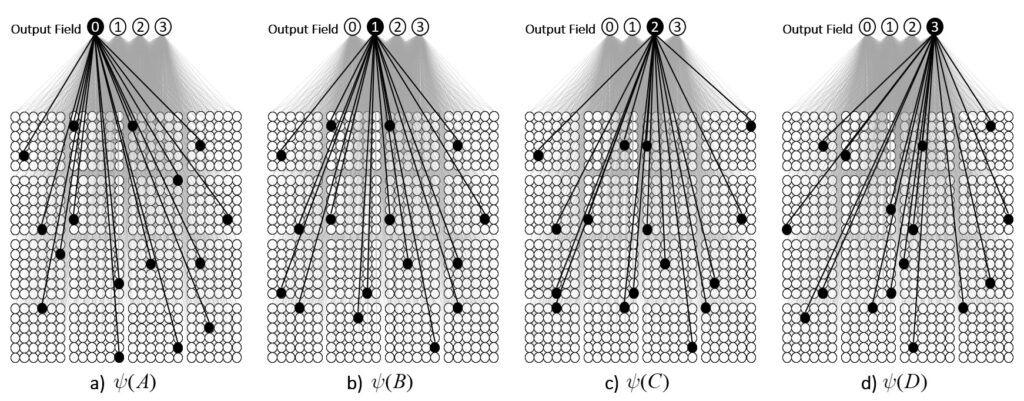
It is possible to represent the states of a physical system as sets, in particular, as sparse sets over binary units, where all states are of the same cardinality Q. Fig. 1 shows four states, A-D, represented by four such sets, ψ(A)-ψ(D). Here the representational field (the universal set), F, is organized as Q=16 winner-take-all (WTA) modules each with K=36 units. All state-representing sets consist of Q active units, one in each of the Q modules.

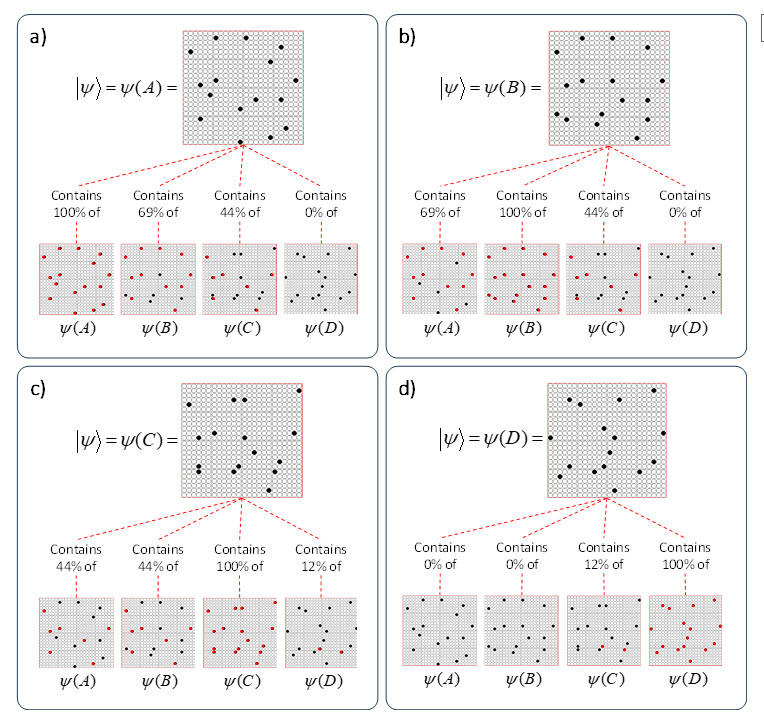
Fig. 1: The representational field, F, is the universal set of bits, partitioned into Q WTA modules, each comprised of K binary units. Every state of the represented physical system, S, is represented by a set of Q active units (black), one per module. We show the representations of four states, A-D, here.

It is possible to represent the similarity of states by the size of their intersection. I’ve chosen these four sets to have a particular pattern of intersections, as shown on Fig. 2: specifically, the sets representing states B, C, and D, have progressively smaller intersections (red units) with the set representing A.  Thus, this similarity measure, which we could call “similarity to A”, is physically reified as this pattern of intersections.

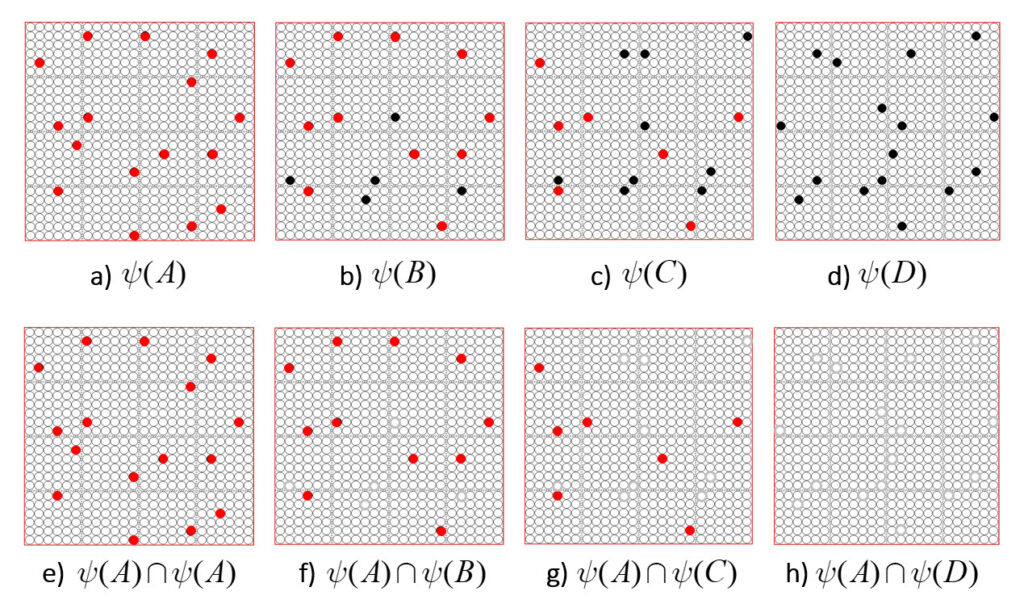
Fig. 2: (top row) Repeats Fig. 1 but with intersections with
ψ(A) highlighted in red. (bottom row) Just showing the intersecting units.

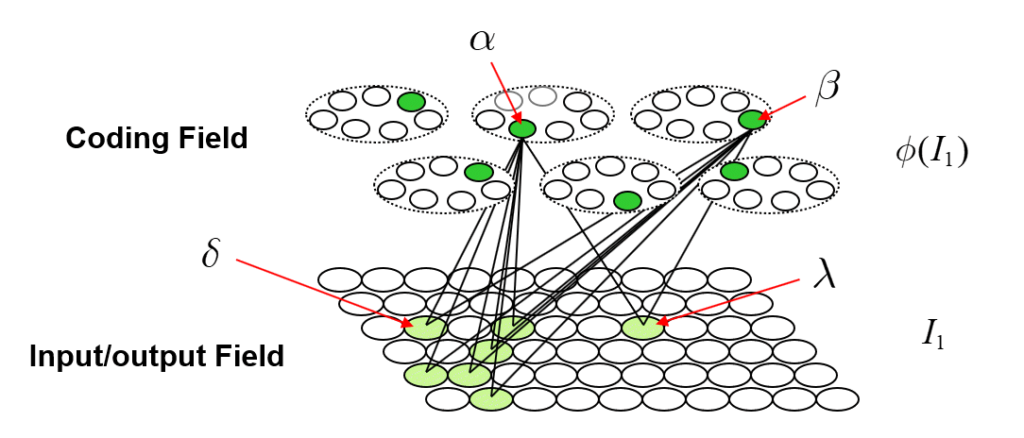
We can imagine a method for reading out the value of this similarity measure.  Specifically, we could have another field of binary units, a simpler field, with just four units, labelled, “0”-“3”, that receives a complete binary matrix from F.  Suppose we activate state A, i.e., turn on its Q units, i.e., the set ψ(A), and at the same time, turn on the output unit “0”, and increase the Q weights from the Q active units to output unit “0”, as in Fig. 3a.  Suppose that at some other time, we activate B, i.e., ψ(B), simultaneously turn on output unit “1”. and increase the Q weights from ψ(B) to “1”, as in Fig. 3b. We do this for states C and D as well, increasing the Q weights from ψ(C) to “2”, and the Q weights from ψ(D) to “3”, as in Figs. 3c,d.

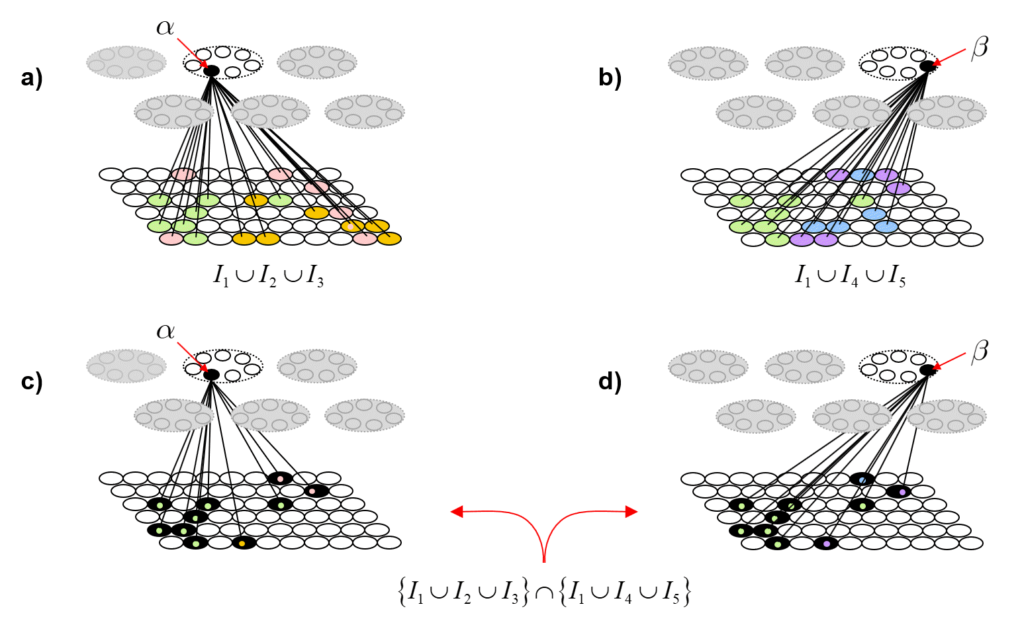
Fig. 3: Increasing the weights from the active set in the state-representing field, F, to the relevant output unit for each of the four defined states, A-D.

Now, having done those four operations in the past, suppose state A again comes into existence, i.e., the set ψ(A) activates, as in Fig. 4a. In this case, because of the weights we increased in that original event in the past (in Fig. 3a), the input summation to output unit “0” will be Q=16, output unit “1” will have summation |ψ(A)∩ψ(B)|=11, “2” will have sum |ψ(A)∩ψ(C)|=7, and “3” will have sum |ψ(A)∩ψ(D)|=0. Suppose we treat the output field as WTA: then, “0” becomes active and the other three remain inactive. In this case, the output field has indicated, i.e., observed, that the physical system is in state A. Note that these summations are due to (caused by): a) the subsets of units that are the intersections of the relevant states; and b) the pattern of weight increases that have been made to the matrix. And note that that pattern of weight increases is necessarily specific to the choices of units that comprise the four sets, ψ(A)-ψ(D).

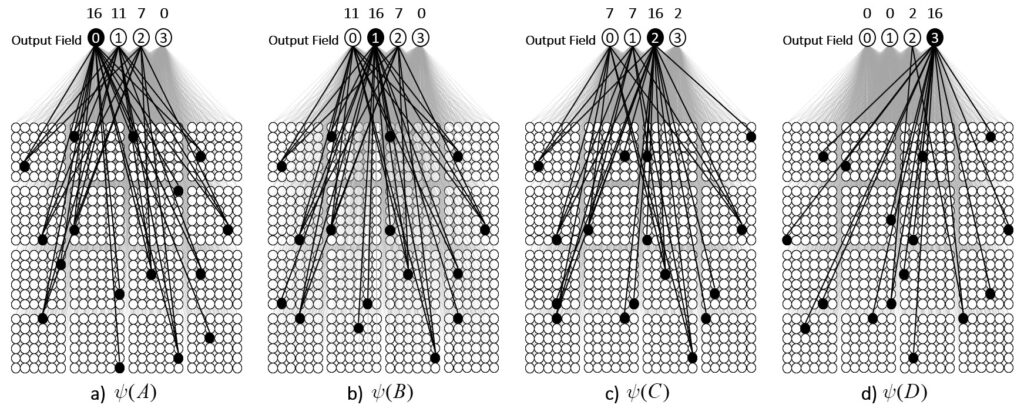
Fig. 4: The input summations (at top) to the output units when each of the four states is presented after the weight increases in Fig. 3 were made.

Thus far, I’ve said only that these four states have a similarity relation that correlates with their representations’ intersection sizes.  But let’s now get more specific and say that these four sets represent the four possible states of a very simple physical system, namely, a universe with one spatial dimension with four discrete positions, A-D, and one particle, x, which can move from one location to an adjacent one on any one time step, as in Fig. 5. Thus it has two properties, location and some basic notion of velocity. In this case, state A can be described as “x is at position A” or “x is distance 0 from A”, state B can be described as “x is at position B”, or “x is distance 1 from A”. Thus, the output unit labels in Figs. 3 and 4 reflect the distances from A. If x was in position A at t (i.e., Fig. 5a) and position B at t+1, then we could describe Fig. 5b as “x is in at position B, moving with speed 1”.

Fig. 5: A tiny 1-dimensional universe with four positions, A-D, and one particle, x, with two properties, location, and some primitive notion of velocity. That is, on any given time step, all it can do it move to an adjacent position, or stay where it is.

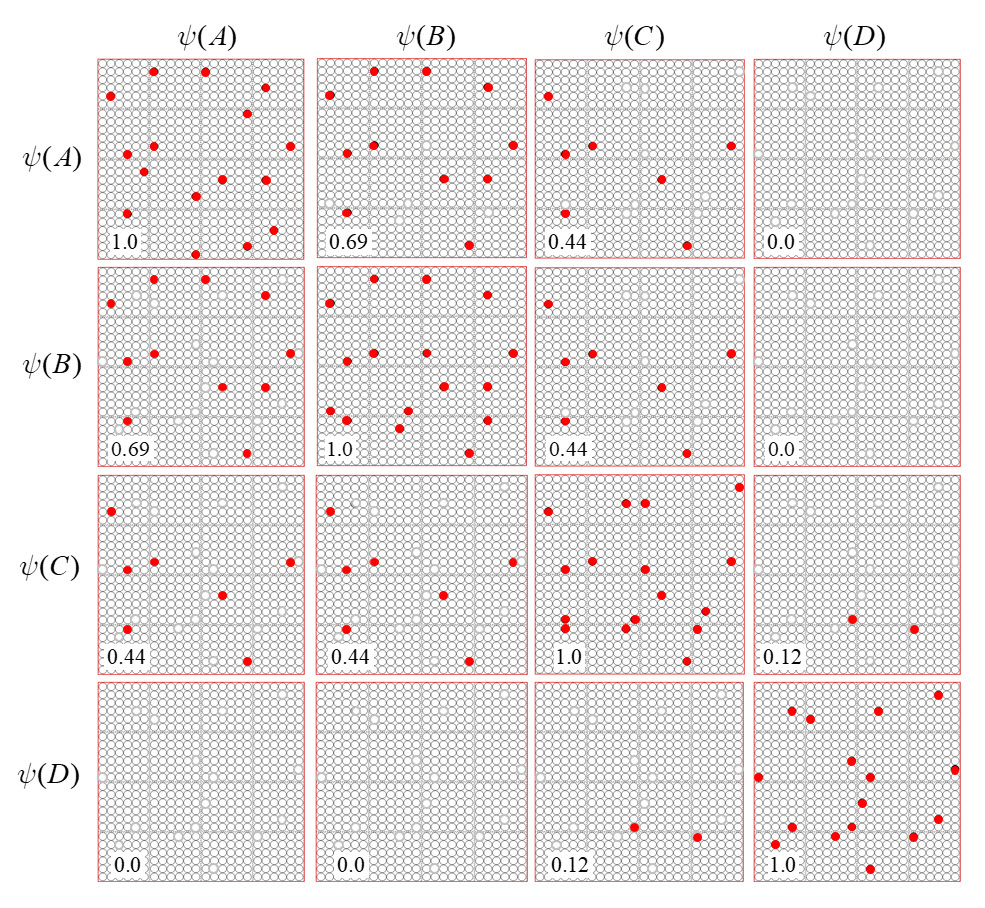
Now, suppose that instead of the output field functioning as WTA, we allow all its units to become active with strength proportional to their input sums normalized by Q.  Then “0” is active at strength 16/16=1, “1” is active at strength 11/16 ≈ 0.69, “2” is active with strength 7/16 ≈ 0.44, and “3” at strength 0/16 = 0.  The vector of output activities constitutes a similarity distribution over the states.  And, if we grant that similarity correlates with likelihood, then it also constitutes a likelihood distribution.  Furthermore, we could easily renormalize this likelihood distribution to a total probability distribution (by adding up the likelihoods and dividing the individual likelihoods by their sum). We can do the same analysis for each of other three states and the summations will be as shown at the top of Figs. 4b-d. Fig. 6 shows the complete pairwise intersection pattern of the four states (sets). The numbers show the fractional activation (likelihood) of a state when the state along the main diagonal is fully active. In all cases, we could normalize these distributions to total probability distributions, which would comport with the physical intuition that given some particular signal (evidence) indicating the position of a particle, progressively further locations should have progressively lower probabilities.

Fig. 6: Pairwise intersections of the states (sets). In each panel, the number is the fractional activation of the state when the state along the main diagonal is active. These numbers can be interpreted as likelihoods of the states, which are normalizable to total probabilities.

The State Update Operator

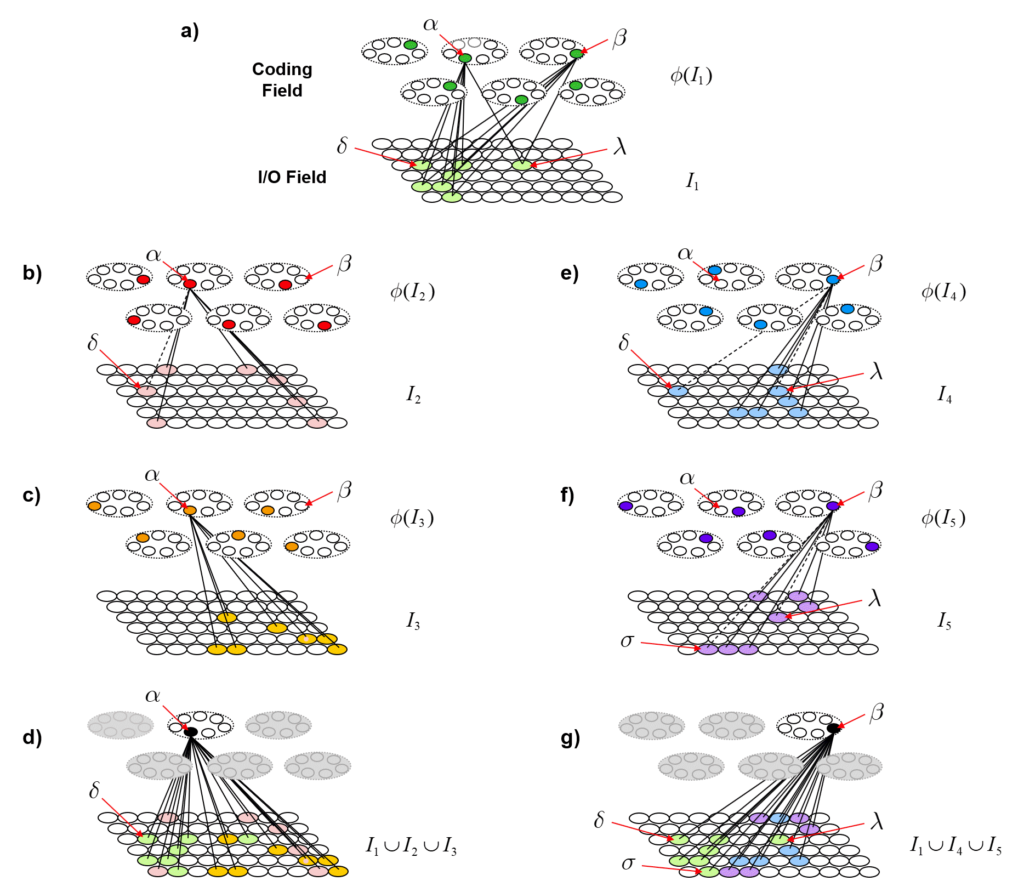
The simple example of Figs. 1-6 provides a mechanistic explanation of how a pattern of set intersections can represent, in fact, physically reify, a similarity measure, i.e., inverse distance measure, or in still other words, a dimension.  But something more is needed.  Specifically, in order for this dimension to truly have the semantics of a spatial dimension, there must be constraints on how the state can change through time.  In Figs. 3 and 4, I’ve introduced a weight matrix to read out the state.  But thus far I’ve provided no mechanism by which the state itself can change through time.  Thus, we need some kind of operator that updates the state.  And, this operator must enforce the natural constraint for a spatial dimension which is that movement along the dimension must be local.  This is fundamental to our notion of what it means to be a spatial dimension.  If, from one time step to the next, the particle could appear anywhere in the universe, then there is no longer any reasonable notion of spatial distance, i.e., all locations are the same distance away from the current location. Remember, the only thing in this universe is the particle x: so there is nothing else that distinguishes the locations except for the presence/absence of x. And, consequently, there is no notion of speed either. For simplicity, we’ll take the constraint to be that the position of the particle can change by at most one position on each time step.  So, what is this operator? It’s a complete matrix of binary weights from F to itself, i.e., a recurrent matrix that connects every one of F’s bits to every one of F’s bits and a rule for how the signals sent via the matrix from the set active at t are used to determine the set that becomes active at t+1. Fig. 7 depicts a subset of the weights comprising this operator (green arcs).

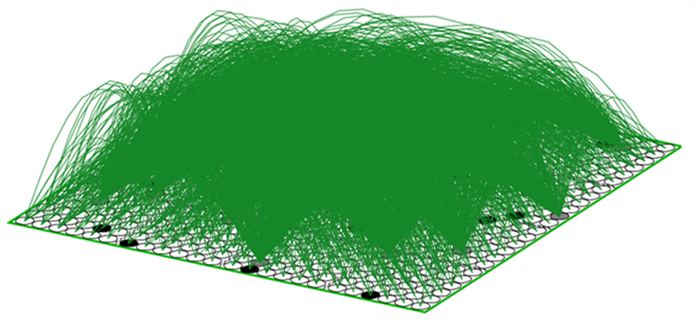
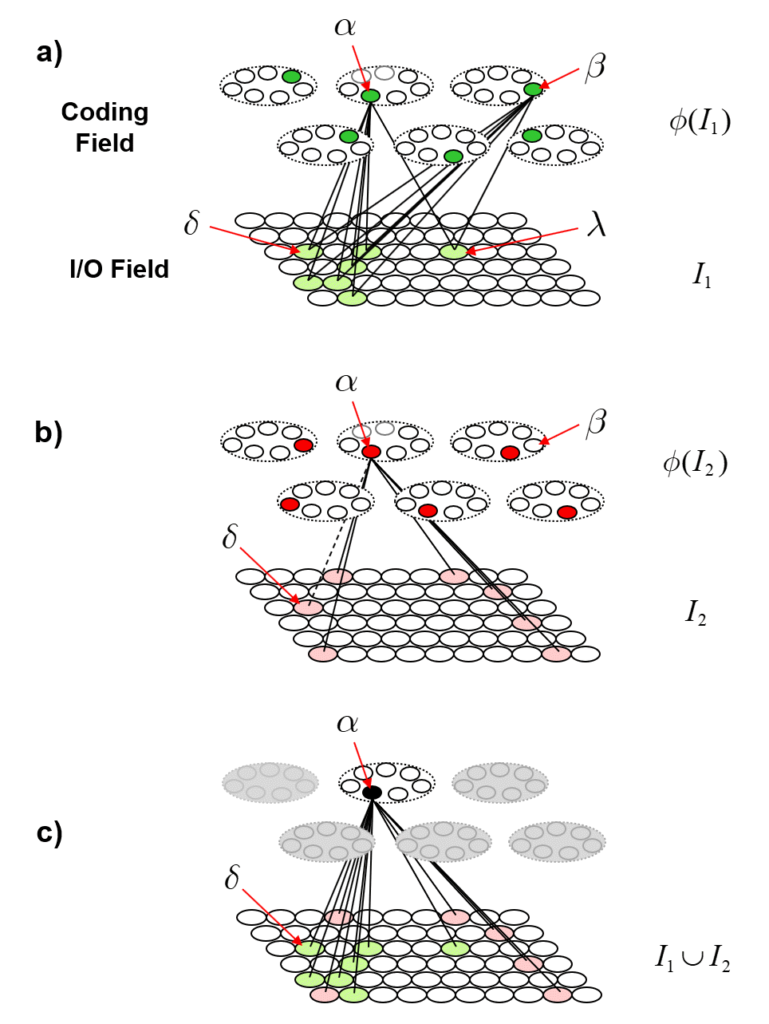
Fig. 7: A depiction of the state-representing field, F, with a particular state (set) active and the complete recurrent binary matrix from F back to itself. Only a subset of the connections are shown (green arcs).

This operator works similarly to the read-out matrix.  On each time step, t, the Q active units comprising the active state, ψ(t), send out signals via the matrix, which arrive back at F at t+1 and give rise to the next state, ψ(t+1).  The algorithm by which the next state is chosen is quite simple: in each of the Q WTA modules, each of the K units evaluates its input summation and the unit with the max sum wins. An essential question is: how do we find a set of weights for the matrix that will enforce the desired dynamics?  Well, imagine all weights are initially 0. Suppose we activate one of the states, say, ψ(A), time t.  Then, at t+1, instead of running the WTA algorithm described above, we instead just manually turn on state ψ(B).  Then, we simply increase all the weights from the Q active units at t to the Q active units at t+1, as in Fig. 8b, where the units active at t, ψ(A), are gray and the units active at t+1, ψ(B), are black. We can imagine doing this for all the other transitions that correspond to local movements: Figs. 8c,d shows this for the transitions from ψ(B) to ψ(C) and from ψ(C) to ψ(D). In this way, we embed the constraints on the system’s dynamics in the weight matrix. I believe that each of these transitions might correspond to Jacob Barandes’s “stochastic microphysical operators”. Having performed these weight increase operations in the past, if ψ(A) ever becomes active in the future, then the update algorithm stated above will compute that each of the Q units comprising ψ(B) has an input sum of 16. Assuming that in such instances, those Q units indeed have the max sum in their respective modules, this will lead to the complete reinstatement of ψ(B). And similarly if we reinstated any of the other states as well.

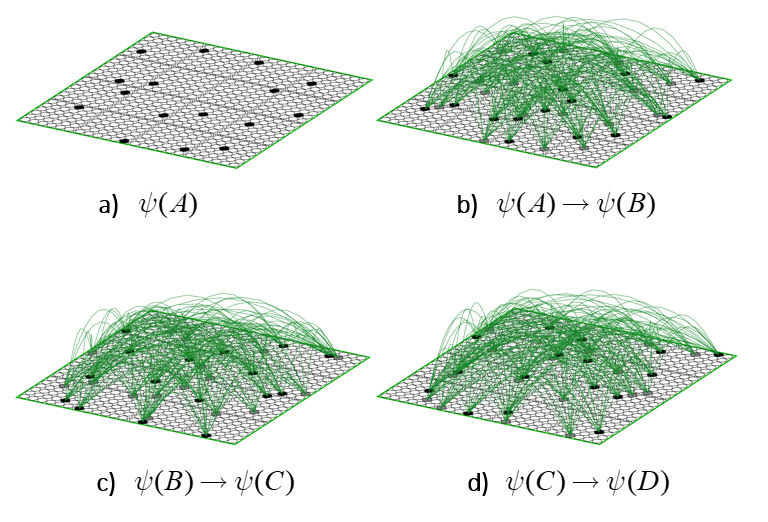
Fig. 8: Depiction of the embedding of some of the state transitions into the matrix, i.e., into the state update operator.

Thus, we see that in this model, we build the operator. More precisely, to fully model a physical system, we need to choose the set of state representations, and we need to find a weight set, which is specific to the chosen sets, which enforces the system’s dynamics.  A natural question then is: is there an efficient computational procedure that can do this?  Yes.  The model, i.e., data structure + algorithm, that can do it has been described multiple times [1-4], as a model of neural computation, specifically, as a model of how information is stored and retrieved in the brain.  Crucially, the algorithm runs in fixed time.  And, with few additional principles / assumptions, the algorithm effectively has linear [“O(N)”] time complexity, where N is the number of states of the system.  We’ll return to that in a later section.

Relation of Set-based formalism to QT’s vector-based formalism

You might be wondering how the model being described here relates to the canonical, vector-based formalism of quantum theory (QT), i.e., based on Hilbert space and the Schrodinger equation. Each of the state-representing sets, ψ(A)-ψ(D), are the basis functions. And, the binary weight matrix, together with the simple algorithm described above, is the operator. But here’s the crucial difference. The basis functions of QT are formally vectors and thus have the semantics of 0-dimensional points. This zero dimensionality, i.e., zero extension, of the represented entity is what allows the formalism to represent a basis state by a single (localized) symbol, i.e., using a localist representation. Fig. 9a shows this for the 4-state system we’ve been using: the four basis functions each has its own dedicated symbol and the four symbols are formally disjoint. But they are not merely formally disjoint: they are physically disjoint in any physical reification of the formalism in which operations are performed. We do not write all these symbols down on top of each other, i.e., superpose them, as in Fig. 9b. That becomes a blur and meaningless, and cannot be operated on by the formal mechanics of QT. Yes, we can abbreviate the fully expanded sum with a single symbol, i.e. the summation symbol (with the relevant indexes), as in Fig. 9c. But again, actual computations, i.e., applications of the Schrodinger equation to update the system, are formally outer products of the fully expanded summations, i.e., requiring 2Nx2N multiplications, where N is the number of basis functions.

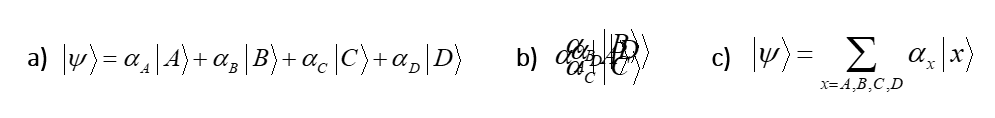
Fig. 9: (a) QT’s fully expanded symbolic representation of a system with four basis states. (b) We do not physically superpose the terms representing the individual basis states: that becomes a meaningless blur. (c) The typical abbreviation of the fully expanded representation using the summation symbol.

Comparing Fig. 10 to Fig. 9 shows the stark representational difference between my theory and QT. Fig. 10a shows the formal symbol, ψ(A), representing state A: it’s the set of Q=16 active (black) bits in the fermionic field. And below it we show the strengths of presence of each of the four basis states in state A (repeated from Fig. 2a). Thus these basis states are not orthogonal as are the basis states in QT’s Hilbert space representation. Again, the physical reification of each individual basis state, i.e., ψ(X), simultaneously both: i) is the state X at full strength because all Q of ψ(X)’s bits are active; and ii) is all the other basis states, with strengths proportional to their intersections with ψ(x).  Thus, unlike the situation for QT (i.e., Fig. 9b), when you look at any one of the four set-based representations in Fig. 10 you are looking at the physical superposition of all the system’s states, just with different degrees of strength for the different states depending on which state is fully active.  This is superposition realized in a purely classical way, as set intersection. There is no blurriness and the active sparse set is directly operated on by the mechanics of the formalism.  And, crucially, that operation consists of a number of atomic operations that depends on the number of physical representational units (the number of bits comprising F), not on the number of represented basis states. Also, unlike the formalism of QT, the representation of the basis states per se and of the probabilities of the states (which in QT are formally probability amplitudes, but in my theory, are formally likelihoods) per se are formally co-mingled: all of the information about the state is distributed out homogeneously throughout all Q of its bits.

Fig. 10: Illustration of the representations of the basis states and of the superposition in the set-based theory. Every basis state is both itself and a superposition of all the states. Panel a depicts the fractional strengths of presence of each of the four states when state A is fully active (i.e., when all Q of ψ(A)’s bits are active). The other panels show this for the three other basis states. In each panel, the red bits are those that intersect with the fully active set.

The stark difference described above all comes down to the fact that in QT, states are represented by vectors but in my theory, they  are represented by sets.  A vector is formally equivalent to a point in the vector space. A point is a 0-dimensional object, i.e., it has no extension. But a set fundamentally does have extension. This is because the elements of a set are unordered (whereas those of a set are ordered).  This means that from an operational standpoint, there is no shorter representation of a set than to explicitly “list”, i.e., explicitly activate, all its elements. While we can assign a single symbol, e.g., “ψ(A)”, as the name of a set, the formal representation of any operation on a set must include symbols representing every element in the set. Thus, to specify the outcome of the application of the state update operator at time t+1, we must show you the full matrix of weights, i.e., the state of every weight, or at least the state of every weight leading from every active element at t, as in Fig. 8. The unorderedness of sets has crucial implications regarding the physical realizations of the formal objects and of the operations on the formal objects. This relates directly to Jacob Barandes’s “category problem” of QT, which concerns the relation between “happening” and “measuring”. See his talk.

..Next Section coming soon…

I’ll continue to explain and elaborate on how the functionality of superposition is fully achieved by classical set intersection. In particular, “fully achieving the functionality” includes achieving the computational efficiency (i.e., exponential speed-up) of quantum superposition.

And, I’ll fully explain the completely classical explanation of entanglement that comes with this theory based on representing states by sparse sets. An essay of mine from 2023 already explains entanglement in my formalism, but it needs updating.

I’ll elaborate on how this core theory generalizes to explain how the three large-scale spatial dimensions of the universe are emergent. This has already been explained at length in an earlier essay (2021), but that also needs significant updating.

I’m continuing to learn a lot about some other quantum foundation theories, i.e., Barandes’ “Indivisible Stochastic Processes”, Finster’s “Causal Fermions”, and “Causal Sets”, and will be elaborating on the relationships that exist between those theories and mine. But, it is immediately clear from their lectures that at least the latter two are vector-based theories (despite their names). And it is true that none of these three theories has yet proposed a physical underpinning of the probabilities, as I have.

References

  1. Rinkus, G., A Combinatorial Neural Network Exhibiting Episodic and Semantic Memory Properties for Spatio-Temporal Patterns, in Cognitive & Neural Systems. 1996, Boston U.: Boston.
  2. Rinkus, G., A cortical sparse distributed coding model linking mini- and macrocolumn-scale functionality. Frontiers in Neuroanatomy, 2010. 4.
  3. Rinkus, G. A Radically New Theory of How the Brain Represents and Computes with Probabilities. in Machine Learning, Optimization, and Data Science. 2024. Champlinaud: Springer Nature Switzerland.
  4. Rinkus, G.J., Sparsey™: event recognition via deep hierarchical sparse distributed codes. Frontiers in Computational Neuroscience, 2014. 8(160)

Representing Entities as Sets Provides a Classical Explanation of Quantum Entanglement

Quantum Computing, quantum entanglement, quantum foundations, Sparse Distributed Representations, , ,

Entanglement is usually described in terms of a physical theory, namely quantum theory (QT), wherein the entities formally represented in the theory are physical entities, e.g., electrons, photons, composites (ensembles) of any size. In contrast, I will describe entanglement in the context of an information processing model in which the entities formally represented in the theory are items of information. Of course, any item of information, even a single bit, is ultimately physically reified somewhere, even if only in the physical brain of a theoretician imagining the item. So, we might expect the two descriptions of entanglement, one in terms of a physical theory and the other in terms of an information processing theory, to coalesce, to become equivalent, cf. Wheeler’s “It from Bit”. This essay works towards that goal.

The information processing model used here is based on representing items of information as sets, specifically, (relatively) small subsets, of binary representational units chosen from a much larger universal set of these units. This type of representation has been referred to as a sparse distributed representation (SDR) or sparse distributed code (SDC). We’ll use the term, SDC. Fig. 1 shows a small toy example of an SDC model. The universal set, or coding field (or memory), is organized as a set of Q=6 groups of K=7 binary units. These groups function in winner-take-all (WTA) fashion and we refer to them as competitive modules (CMs). The coding field is completely connected to an input field of binary units, organized as a 2D array (e.g., a primitive retina of binary pixels), in both directions, a forward matrix of binary connections (weights) and a reverse matrix of binary weights. All weights are initially zero. We impose the constraint that all inputs have the same number of active pixels, S=7.

Fig. 1: Small example of an SDC-based model. The coding field consists of Q=6 competitive modules (CMs), each consisting of K=7 binary units. The input field is a 2D array of binary units (pixels) and is completely connected in both directions, i.e., a forward and a reverse matrix of binary weights (grey lines, each on represents both the forward and the reverse weight).

The storage (learning) operation is as follows. When an input item, Ii, is presented (activated in the input field), a code, φ(Ii) consisting of Q units, one in each of the Q CMs, is chosen and activated and all forward and reverse weights between active input and active coding field units are set to one. In general, some of those weights may already be one due to prior learning. We will discuss the algorithm for choosing the codes during learning in a later section. For now, we can assume that codes are chosen at random. In general, any given coding unit, α, will be included in the codes of multiple inputs. For each new input in whose code α is included, if that input includes units (pixels) that were not active in any of the prior inputs in whose codes α was included, the weights from those pixels to α will be increased. Thus, the set of input units having a connection with weight one onto α can only increase with time (with further inputs). We call that set of input units with w=1 onto α, α’s tuning function (TF),

The retrieval operation is as follows. An input, i.e., a retrieval cue, is presented, which causes signals to travel to the coding field via the forward matrix, whereupon the coding field units compute their input summations and the unit with the max sum in each CM is chosen winner, ties broken at random. Once this “retrieved” code is activated, it sends signals via the reverse matrix, whereupon, the input units compute their input summations and are activated (or possibly deactivated) depending on whether a threshold is exceeded. In this way, partial input cues, i.e., with less than S active units, can be “filled in” and novel cues that are similar enough to previously (learned) inputs can cause the codes of such closest-matching learned inputs to activate, which can then cause (via the reverse signals) activation of that closest-matching learned input.

With the above description of the model’s storage and retrieval operations in mind, I will now describe the analog of quantum entanglement in this classical model. Fig. 2 shows the event of storing the first item of information, I1, into this model. I1 consists of the S=7 light green input units. The Q=6 green coding field units are chosen randomly to be I1‘s code, φ(I1), and the black lines show some of the QxS=42 weights that would be increased, from 0 to 1, in this learning event. Each line represents both the forward and reverse weight connecting the two units. More specifically, the black lines show all the forward/reverse weights that would be increased for two of φ(I1)’s units, denoted α and β. Note that immediately following this learning event (the storage of I1), α and β have exactly the same TF. In fact, all six units comprising φ(I1) have exactly the same TF. In the information processing realm, and more pointedly in neural models, we would describe these six units as being completely correlated. That is, all possible next inputs to the model, a repeat presentation of I1 or any other possible input, would cause exactly the same input summation to occur in all six units, and thus, exactly the same response by all six units. In other words, all six units carry exactly the same information, i.e., are completely redundant.

Fig. 2: The first input to the model, I1, consisting of the S=7 light green units, has been presented and a code, φ(I1), consisting of Q=6 units (green), has been chosen at random. All forward and reverse weights between active input and coding fields units are set to one. The black lines show all such weights involving coding units α and β.

As the reader may already have anticipated, I will claim that these six units are completely entangled. We can consider the act of assigning the six units as the code, φ(I1), as analogous to an event in which a particle decays, giving rise, for example, to two completely entangled photons. In the moment when the two particles are born out of the vacuum, they are completely entangled and likewise, in the moment when the code, φ(I1), is formed, the six units comprising it are completely entangled. However, in the information processing model described here, the mechanism that explains the entanglement, i.e., the correlation, is perfectly clear: it’s the correlated increases to the forward/reverse weights to/from the six units, which entangles those units. Note in particular, that there are no direct physical connections between coding field units in different CMs. This is crucial: it highlights the fact that in this explanation of entanglement, the hidden variables are external, i.e., non-local, to the units that are entangled. The hidden variables ARE the connections (weights). This hints at the possibility that the explanation of entanglement herein comports with Bell’s theorem. The 2015 results proving Bell’s theorem, explicitly rule out only local hidden variables explanations of entanglement. Fig. 3 shows the broad correspondence between the information theory and the physical theory proposed here.

Fig. 3: Broad correspondence between the information processing theory described here (and previously throughout my work) and the proposed physical theory. This figure will generalized in a later section to include the recurrent matrix that connects the coding field to itself (and is also part of the bosonic representation), which is needed to explain how the physical state represented by the coding field is updated through time, i.e. the dynamics.

Suppose we now activate just one of the seven input units comprising I1, say δ. Then φ(I1) will activate in its entirety (i.e., all Q=6 of its units) due to the “max sum” rule stated above, and then the remaining six input units comprising I1 will be activated based on the inputs via the reverse matrix. Suppose we consider the activation of δ to be analogous to making a measurement or observation. In this interpretation, the act of measuring at one locale of the input field, at δ, immediately determines the state of the entire coding field and subsequently (via the reverse projection) the entire state of the input field [or more properly, input/output (“I/O”) field], in particular, the state of the spatially distant I/O unit, λ. Note that there is no direct connection between δ and λ. The causal and deterministic signaling went, in one hop, via the connections of the forward and reverse matrices. Thus, while our hidden variables, the connections, are strictly external (non-local) to the units being entangled (i.e., the connections are not inside any of the units, either coding units or I/O units), they themselves are local in the sense of being immediately adjacent to the entangled units. Thus, this explanation meets the criteria for local realism. This highlights an essential assumption of my overall explanation of quantum entanglement. It requires that physical space, or rather the underlying physical substrate from which our apparent 3D space and all the things in it emerge, be composed of smallest functional units that are completely connected. In another essay, I call these smallest functional, or atomic functional, units, “corpuscles”. Specifically, a corpuscle is comprised of a coding field similar to, but vastly larger than (e.g., Q=106, K=1015), those depicted here and: a) a recurrent matrix of weights that completely connects the coding field to itself; and b) matrices that completely connect the coding field to the coding fields in all immediately neighboring corpuscles. In particular, the recurrent matrix allows the state of the coding field at T to influence, in one signal-propagation step, the state of the coding field at T+1. Thus, to be clear, the explanation of entanglement given here applies within any given corpuscle. It allows instantaneous, i.e., faster than light, transmission of effects throughout the region of (emergent) space corresponding to the corpuscle, which I’ve proposed elsewhere to be perhaps 1015 Planck lengths in diameter. If we define the time, in Planck times, that it takes for the corpuscle to update its state to equal the diameter of corpuscle, in Planck lengths, then signals (effects) are limited to propagating across larger expanses, i.e., from one corpuscle to the next, no faster than light.

Here I must pause to clarify the analogy. In the typical description of entanglement within the context of the standard model (SM), it is (typically) the fundamental particles of the SM, e.g., electrons, photons, which become entangled. In the explanation described here, it is the individual coding units that become entangled. But I do not propose that that these coding field units are analogous to individual fundamental particles of the standard model (SM). Rather, I propose that the fundamental particles of the SM correspond to sets of coding field units, in particular, to sets of size smaller than a full code, i.e., smaller than Q. That is, the entire state of the region of space emerging from a single corpuscle is a set of Q active coding units. But a subset of those Q units might be associated with any particular entity (particle) present in that region at any given time. For example, a particular set of coding units, say of size Q/10, might always be active whenever an electron is present in the region, i.e., that “sub-code” appears as a subset in all full codes (of size, Q) in which an electron is present. Thus, rather than saying that, in the theory described here, individual coding units become entangled, we can slightly modify it to say that subsets of coding units become entangled.

Returning to the main thread, Fig. 4 now describes how patterns of entanglement generally change over time. Fig. 4a is a repeat of Fig. 2, showing the model after the first item, I1, is stored. Fig. 4b shows a possible next input, I2, also consisting of S=7 active I/O units, one of which, δ is common to I1. Black lines depict the connections whose weights are increased in this event. The dotted line is to indicate that the weights between α and δ will have been increased when I1 was presented. Fig. 4c shows α’s TF after I2 was presented. It now includes the 13 I/O units in the union of the two input patterns, {I1 ∪ I2}. In particular, note that coding units, α and β are no longer completely correlated, i.e., their TFs are no longer identical, which means that we could find new inputs that elicit different responses in α and β. In general, the different responses, can lead, via reverse signals, to different patterns of activation in the I/O field, i.e., different values of observables. In other words, they are no longer completely entangled. This is analogous to two particles which arise completely entangled from a single event, going off and having different histories of interactions with the world. With each new interaction that either one has, they become less entangled. However, note that even though α and β are no longer 100% correlated, we can still predict either’s state of activation based on the other’s at better-than-chance accuracy, due to the common units in their TFs and to the corresponding correlated changes to their weights.

Fig. 4: (a) Repeat of Fig. 2 for reference. (b) Presentation of the second input, I2, its randomly selected code, φ(I2), and the new learning involving coding unit α. The weights to/from I/O unit δ are dashed since they were already increased to one when I1 was presented, i.e., δ was active in both inputs. (c) α’s TF is the union of all I/O units that are active in any input in whose code α was included. In particular, α and β are no longer completely entangled (correlated), due to this additional interaction α has had with the world.

Fig. 5 now shows a more extensive example illustrating the further evolution of the same process shown in Fig. 4. In Fig. 5, we show coding unit α participating in a further code, φ(I3), for input I3. And we show coding unit β participating in the codes of two other inputs, I4 and I5, after participating, along with α, in the code of the first input, I1. Panel d shows the final TF for α after being used in codes of three inputs, I1, I2 and I3. Panel g shows the final TF for β after being used in the codes for I1, I4 and I5. One can clearly see how the TFs gradually diverge due to their diverging histories of usage (i.e., interaction with the world). This corresponds to α and β becoming progressively less entangled with successive usages (interactions).

Fig. 5: Depiction of the continued diminution of the entanglement of α and β as they participate in different histories of inputs. Panel d shows the final TF for α after being used in codes of three inputs, I1, I2 and I3. Panel g shows the final TF for β after being used in the codes for I1, I4 and I5.

To quantify the decrease in entanglement precisely, we need to do a lot of counting. Fig. 6 shows the idea. Figs. 6a and 6b repeat Figs. 5d and 5g, showing the TFs of α and β. Figs. 6c and 6d show the intersection of those two TFs. The colored dots indicate the input from which the particular I/O unit (pixel) was accrued into the TF. In order for any future input [including any repeat of any of the learned (stored) ones] to affect α and β differently (i.e., to cause α and β to have different input sums, and thus, to have different chances of winning in their respective CMs, and thus, to ultimately cause activation of different full codes), that code must include at least one I/O unit that is in either TF but not in the intersection of the TFs. Again, all inputs are constrained to be of size S=7. Thus, after presenting any input, we can count the number of such codes that meet that criterion. Over long histories, i.e., for large sets of inputs, that number will grow with each successive input.

Fig. 6: (a,b) Repeats of Figs. 5d and 5g showing the TFs of α and β. (c,d) The union of the two TFs (black cells). The colored dots tell from which input the I/O unit (pixel) was accrued into the relevant coding unit’s TF.

A storage (learning) algorithm that preserves similarity

In the examples above, the codes were chosen randomly. While we can and did provide an explanation of entanglement under that assumption, a much more powerful and sweeping physical theory emerges if we can provide a tractable mechanism (algorithm) for choosing codes in a way that statistically preserves similarity, i.e., maps similar inputs to similar codes. In this section, I will describe that algorithm. The final section will then revisit entanglement, providing further elaboration.